8. Assessing Product Reliability
8.1. Introduction
8.1.6. What are the basic lifetime distribution models used for non-repairable populations?

8.1.6.5.

Gamma

Formulas for the gamma model

Formulas and Plots

There are two ways of writing (parameterizing) the gamma distribution that are common in the literature. In addition, different authors use different symbols for the shape and scale parameters. Below we show two ways of writing the gamma, with "shape" parameter \(a = \alpha\), and "scale" parameter \(b = 1/\beta\).

$$ \begin{array}{ll} \mbox{PDF:} & f(t, a, b) = \frac{b^a}{\Gamma(a)}t^{a-1} e^{-bt} \\ & \\ & f(t, \alpha, \beta) = \frac{1}{\beta^{\alpha}\Gamma(\alpha)}t^{\alpha-1}e^{-t/\beta} \\ & \\ \mbox{CDF:} & F(t) = \int \limits_{0}^{t} f(t)dt \\ & \\ \mbox{Reliability:} & R(t) = 1 - F(t) \\ & \\ \mbox{Failure Rate:} \,\, & h(t) = f(t)/R(t) \\ & \\ \mbox{Mean:} & a/b \mbox{ or } \alpha \beta \\ & \\ \mbox{Variance:} & a/b^2 \mbox{ or } \alpha \beta^2 \end{array} $$

The exponential is a special case of the gamma

Note: When \(a\) = 1, the gamma reduces to an exponential distribution with \(b = \lambda\).

Another well-known statistical distribution, the Chi-Square, is also a special case of the gamma. A Chi-Square distribution with \(n\) degrees of freedom is the same as a gamma with \(a = n\)/2 and \(b\) = 0.5 (or \(\beta\) = 2).

The following plots give examples of gamma PDF, CDF and failure rate shapes.

Shapes for gamma data

Gamma CDF shapes

Gamma failure rate shapes

The gamma is used in "Standby" system models and also for Bayesian reliability analysis

Uses of the Gamma Distribution Model

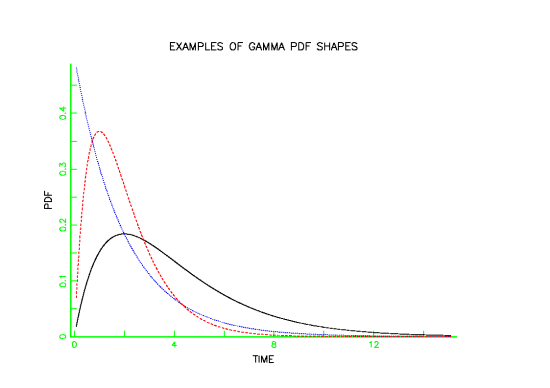
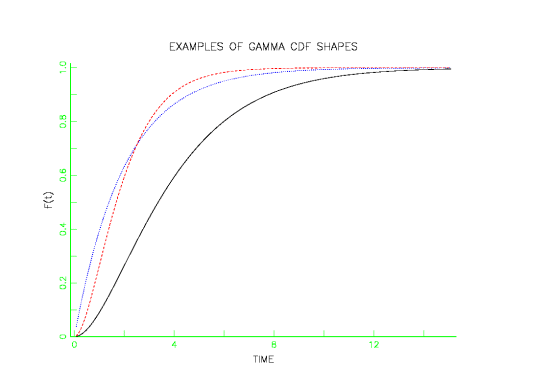
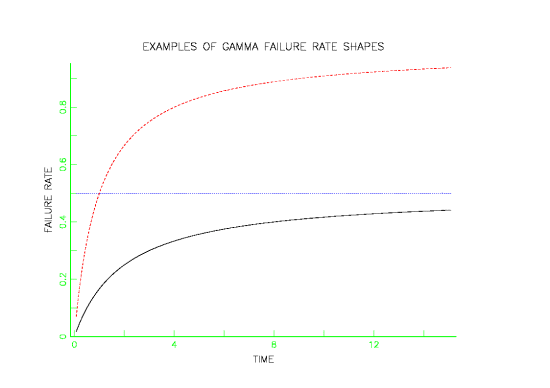
1. The gamma is a flexible life distribution model that may offer a good fit to some sets of failure data. It is not, however, widely used as a life distribution model for common failure mechanisms.
2. The gamma does arise naturally as the time-to-first fail distribution for a system with standby exponentially distributed backups. If there are \(n\)-1 standby backup units and the system and all backups have exponential lifetimes with parameter \(\lambda\), then the total lifetime has a gamma distribution with \(a = n\) and \(b = \lambda\). Note: when \(a\) is a positive integer, the gamma is sometimes called an Erlang distribution. The Erlang distribution is used frequently in queuing theory applications.
3. A common use of the gamma model occurs in Bayesian reliability applications. When a system follows an HPP (exponential) model with a constant repair rate \(\lambda\), and it is desired to make use of prior information about possible values of \(\lambda\), a gamma Bayesian prior for \(\lambda\) is a convenient and popular choice.

Gamma probability plot

We generated 100 random gamma data points using shape parameter \(\alpha\) = 2 and scale parameter \(\beta\) = 30. A gamma probability plot of the 100 data points is shown below.

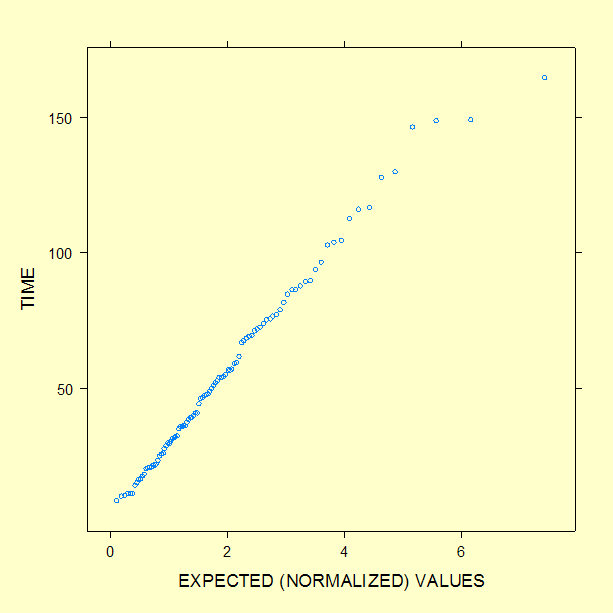
The value of the shape parameter \(\alpha\) can be estimated from data using $$ \hat{\alpha} = \left[ \frac{\bar{t}}{s_t} \right]^2 $$ the squared ratio of mean failure time to the standard deviation of the failure times.

Using an example solved in the section on standby models, where \(\alpha\) = 2, \(\beta\) = 30, and \(t\) = 24 months, the PDF, CDF, reliability, and failure rate are the following.

   PDF = 0.01198
   CDF = 0.19121
   Reliability = 0.80879
   Failure Rate = 0.01481

Functions for computing gamma distribution PDF values, CDF values, reliability values, failure rates, and for producing probability plots, are found in both Dataplot code and R code.