8.1. Introduction
8.1.6. What are the basic lifetime distribution models used for non-repairable populations?
8.1.6.6. |
Fatigue life (Birnbaum-Saunders) |
The PDF, CDF, mean, and variance for the Birnbaum-Saunders distribution are shown below. The parameters are: \(\gamma\), a shape parameter; and \(\mu\), a scale parameter. These are the parameters we will use in our discussion, but there are other choices also common in the literature (see the parameters used for the derivation of the model). $$ \begin{array}{ll} \mbox{PDF:} & f(t) = \frac{1}{2 \mu^2 \gamma^2\sqrt{\pi}} \left( \frac{t^2 - \mu^2}{\sqrt{\frac{t}{\mu}} - \sqrt{\frac{\mu}{t}}} \right) \mbox{exp} \left[ -\frac{1}{\gamma^2} \left( \frac{t}{\mu} + \frac{\mu}{t} -2 \right) \right] \\ & \\ \mbox{CDF:} & F(t) = \Phi \left( \frac{1}{\gamma} \left[ \sqrt{\frac{t}{\mu}} - \sqrt{\frac{\mu}{t}} \, \right] \right) \\ & \\ & \Phi(z) \mbox{denotes the standard normal CDF.} \\ & \\ \mbox{Mean:} & \mu \left( 1 + \frac{\gamma^2}{2} \right) \\ & \\ \mbox{Variance:} & \mu^2 \gamma^2 \left( 1 + \frac{5 \gamma^2}{4} \right) \end{array} $$ PDF shapes for the model vary from highly skewed and long tailed (small gamma values) to nearly symmetric and short tailed as gamma increases. This is shown in the figure below.
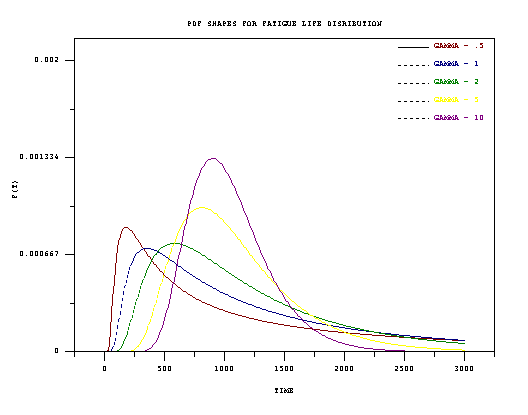
Corresponding failure rate curves are shown in the next figure.
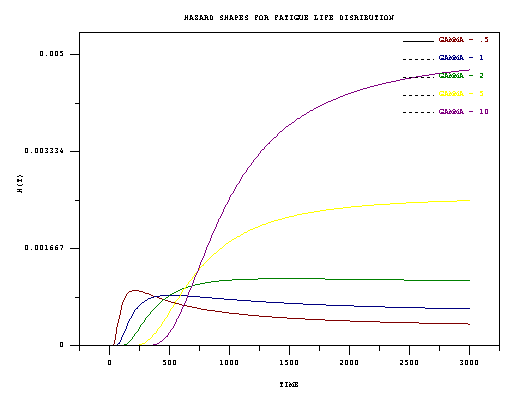
Consider a material that continually undergoes cycles of stress loads. During each cycle, a dominant crack grows towards a critical length that will cause failure. Under repeated application of \(n\) cycles of loads, the total extension of the dominant crack can be written as $$ W_n = \sum_{j=1}^n Y_j \, , $$ and we assume the \(Y_j\) are independent and identically distributed non-negative random variables with mean \(\mu\) and variance \(\sigma^2\). Suppose failure occurs at the \(N\)-th cycle, when \(W_n\) first exceeds a constant critical value \(w\). If \(n\) is large, we can use a central limit theorem argument to conclude that $$ \mbox{Pr}(N \le n) = 1 - \mbox{Pr} \left( \sum_{j=1}^n Y_j \le w \right) = \Phi \left( \frac{\mu \sqrt{n}}{\sigma} - \frac{w}{\sigma \sqrt{n}} \right) \, . $$ Since there are many cycles, each lasting a very short time, we can replace the discrete number of cycles \(N\) needed to reach failure by the continuous time \(t_f\) needed to reach failure. The CDF \(F(t)\) of \(t_f\) is given by $$ F(t) = \Phi \left\{ \frac{1}{\alpha} \left[ \sqrt{\frac{t}{\beta}} - \sqrt{\frac{\beta}{t}} \right] \right\} \, , $$ for appropriate choice of $$ \alpha = \frac{\sigma}{\sqrt{\mu w}} \,\, \mbox{ and } \,\, \beta = \frac{w}{\mu} \,\, .$$ Here \(\Phi\) denotes the standard normal CDF. Writing the model with parameters \(\alpha\) and \(\beta\) is an alternative way of writing the Birnbaum-Saunders distribution that is often used (\(\alpha = \gamma\) and \(\beta = \mu\), as compared to the way the formulas were parameterized earlier in this section).
Note:
The critical assumption in the derivation, from a physical point of
view, is that the crack growth during any one cycle is independent of the
growth during any other cycle. Also, the growth has approximately the same
random distribution, from cycle to cycle. This is a very different situation
from the proportional degradation argument used to derive a log normal
distribution model, with the rate of degradation at any point in time depending
on the total amount of degradation that has occurred up to that time.
The PDF value at time \(t\) = 4000 for a Birnbaum-Saunders (fatigue life) distribution with parameters \(\mu\) = 5000 and \(\gamma\) = 2 is 4.987e-05 and the CDF value is 0.455.
Functions for computing Birnbaum-Saunders distribution PDF values, CDF values, and for producing probability plots, are found in both Dataplot code and R code.

