8. Assessing Product Reliability
8.1. Introduction
8.1.8. How can you evaluate reliability from the "bottom-up" (component failure mode to system failure rate)?

8.1.8.3.

Parallel or redundant model

The parallel model assumes all n components that make up a system operate independently and the system works as long as at least  one component still works

The opposite of a series model, for which the first component failure causes the system to fail, is a parallel model for which all the components have to fail before the system fails. If there are \(n\) components, any (\(n - 1\)) of them may be considered redundant to the remaining one (even if the components are all different). When the system is turned on, all the components operate until they fail. The system reaches failure at the time of the last component failure.

The assumptions for a parallel model are:

1. All components operate independently of one another, as far as reliability is concerned.
2. The system operates as long as at least one component is still operating. System failure occurs at the time of the last component failure.
3. The CDF for each component is known.

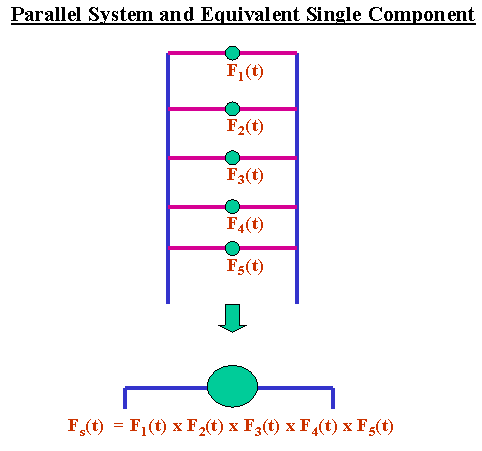
Multiply component CDF's to get the system CDF for a parallel model

For a parallel model, the CDF \(F_S(t)\) for the system is just the product of the CDFs \(F_i(t)\) for the components, or $$ F_S(t) = \prod_{i=1}^n F_i(t) \,\, . $$ \(R_S(t)\) and \(h_S(t)\) can be evaluated using basic definitions, once we have \(F_S(t)\).

The schematic below represents a parallel system with 5 components and the (reliability) equivalent 1 component system with a CDF \(F_S(t)\) equal to the product of the 5 component CDFs.