1.1.6. An EDA/Graphics Example

1. Exploratory Data Analysis
1.1. EDA Introduction

1.1.6. An EDA/Graphics Example

Anscombe Example

A simple, classic (Anscombe) example of the central role that graphics play in terms of providing insight into a data set starts with the following data set :

Data

  X              Y
10.00           8.04
 8.00           6.95
13.00           7.58
 9.00           8.81
11.00           8.33
14.00           9.96
 6.00           7.24
 4.00           4.26
12.00          10.84
 7.00           4.82
 5.00           5.68

Summary Statistics

If the goal of the analysis is to compute summary statistics plus determine the best linear fit for Y as a function of X, the results might be given as:

The above quantitative analysis, although valuable, gives us only limited insight into the data.

Scatter Plot

In contrast, the following simple scatter plot of the data

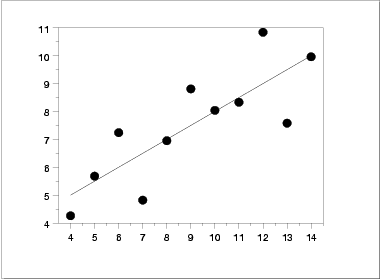
A scatter plot of the Anscombe data

suggests the following:

The data set "behaves like" a linear curve with some scatter;
there is no justification for a more complicated model (e.g., quadratic);
there are no outliers;
the vertical spread of the data appears to be of equal height irrespective of the X-value; this indicates that the data are equally-precise throughout and so a "regular" (that is, equi-weighted) fit is appropriate.

Three Additional Data Sets

This kind of characterization for the data serves as the core for getting insight/feel for the data. Such insight/feel does not come from the quantitative statistics; on the contrary, calculations of quantitative statistics such as intercept and slope should be subsequent to the characterization and will make sense only if the characterization is true. To illustrate the loss of information that results when the graphics insight step is skipped, consider the following three data sets [Anscombe data sets 2, 3, and 4]:

 X2     Y2       X3     Y3       X4     Y4
10.00   9.14    10.00   7.46     8.00   6.58
 8.00   8.14     8.00   6.77     8.00   5.76
13.00   8.74    13.00  12.74     8.00   7.71
 9.00   8.77     9.00   7.11     8.00   8.84
11.00   9.26    11.00   7.81     8.00   8.47
14.00   8.10    14.00   8.84     8.00   7.04
 6.00   6.13     6.00   6.08     8.00   5.25
 4.00   3.10     4.00   5.39    19.00  12.50
12.00   9.13    12.00   8.15     8.00   5.56
 7.00   7.26     7.00   6.42     8.00   7.91
 5.00   4.74     5.00   5.73     8.00   6.89

Quantitative Statistics for Data Set 2

A quantitative analysis on data set 2 yields

which is identical to the analysis for data set 1. One might naively assume that the two data sets are "equivalent" since that is what the statistics tell us; but what do the statistics not tell us?

Quantitative Statistics for Data Sets 3 and 4

Remarkably, a quantitative analysis on data sets 3 and 4 also yields

which implies that in some quantitative sense, all four of the data sets are "equivalent". In fact, the four data sets are far from "equivalent" and a scatter plot of each data set, which would be step 1 of any EDA approach, would tell us that immediately.

Scatter Plots

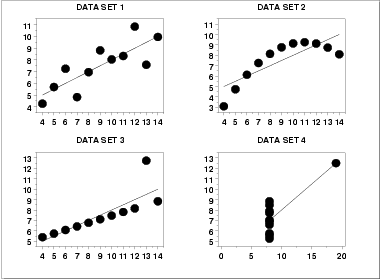
4 scatter plots that exhibit different characteristcs

Interpretation of Scatter Plots

Conclusions from the scatter plots are:

data set 1 is clearly linear with some scatter.
data set 2 is clearly quadratic.
data set 3 clearly has an outlier.
data set 4 is obviously the victim of a poor experimental design with a single point far removed from the bulk of the data "wagging the dog".

Importance of Exploratory Analysis

These points are exactly the substance that provide and define "insight" and "feel" for a data set. They are the goals and the fruits of an open exploratory data analysis (EDA) approach to the data. Quantitative statistics are not wrong per se, but they are incomplete. They are incomplete because they are numeric summaries which in the summarization operation do a good job of focusing on a particular aspect of the data (e.g., location, intercept, slope, degree of relatedness, etc.) by judiciously reducing the data to a few numbers. Doing so also filters the data, necessarily omitting and screening out other sometimes crucial information in the focusing operation. Quantitative statistics focus but also filter; and filtering is exactly what makes the quantitative approach incomplete at best and misleading at worst.

The estimated intercepts (= 3) and slopes (= 0.5) for data sets 2, 3, and 4 are misleading because the estimation is done in the context of an assumed linear model and that linearity assumption is the fatal flaw in this analysis.

The EDA approach of deliberately postponing the model selection until further along in the analysis has many rewards, not the least of which is the ultimate convergence to a much-improved model and the formulation of valid and supportable scientific and engineering conclusions.