1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.3. Graphical Techniques: Alphabetic

1.3.3.2.

Bihistogram

Purpose:
Check for a change in location, variation, or distribution

The bihistogram is an EDA tool for assessing whether a before-versus-after engineering modification has caused a change in

• location;
• variation; or
• distribution.

It is a graphical alternative to the two-sample t-test. The bihistogram can be more powerful than the t-test in that all of the distributional features (location, scale, skewness, outliers) are evident on a single plot. It is also based on the common and well-understood histogram.

Sample Plot:
This bihistogram reveals that there is a significant difference in ceramic breaking strength between batch 1 (above) and batch 2 (below)

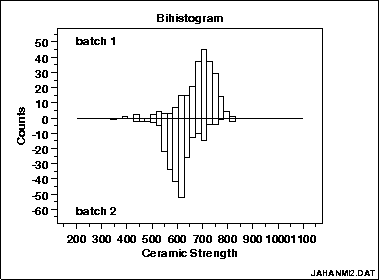
From the above bihistogram of the JAHANMI2.DAT data set, we can see that batch 1 is centered at a ceramic strength value of approximately 725 while batch 2 is centered at a ceramic strength value of approximately 625. That indicates that these batches are displaced by about 100 strength units. Thus the batch factor has a significant effect on the location (typical value) for strength and hence batch is said to be "significant" or to "have an effect". We thus see graphically and convincingly what a t-test or analysis of variance would indicate quantitatively.

With respect to variation, note that the spread (variation) of the above-axis batch 1 histogram does not appear to be that much different from the below-axis batch 2 histogram. With respect to distributional shape, note that the batch 1 histogram is skewed left while the batch 2 histogram is more symmetric with even a hint of a slight skewness to the right.

Thus the bihistogram reveals that there is a clear difference between the batches with respect to location and distribution, but not in regard to variation. Comparing batch 1 and batch 2, we also note that batch 1 is the "better batch" due to its 100-unit higher average strength (around 725).

Definition:
Two adjoined histograms

Bihistograms are formed by vertically juxtaposing two histograms:

• Above the axis: Histogram of the response variable for condition 1
• Below the axis: Histogram of the response variable for condition 2

Questions

The bihistogram can provide answers to the following questions:

1. Is a (2-level) factor significant?
2. Does a (2-level) factor have an effect?
3. Does the location change between the 2 subgroups?
4. Does the variation change between the 2 subgroups?
5. Does the distributional shape change between subgroups?
6. Are there any outliers?

Importance:
Checks 3 out of the 4 underlying assumptions of a measurement process

The bihistogram is an important EDA tool for determining if a factor "has an effect". Since the bihistogram provides insight into the validity of three (location, variation, and distribution) out of the four (missing only randomness) underlying assumptions in a measurement process, it is an especially valuable tool. Because of the dual (above/below) nature of the plot, the bihistogram is restricted to assessing factors that have only two levels. However, this is very common in the before-versus-after character of many scientific and engineering experiments.

Related Techniques

t test (for shift in location)
F test (for shift in variation)
Kolmogorov-Smirnov test (for shift in distribution)
Quantile-quantile plot (for shift in location and distribution)

Case Study

The bihistogram is demonstrated in the ceramic strength data case study.

Software

The bihistogram is not widely available in general purpose statistical software programs. Bihistograms can be generated using Dataplot and R software.