Next Page Previous Page Home Tools & Aids Search Handbook

1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.5. Quantitative Techniques
1.3.5.17. Detection of Outliers

1.3.5.17.2.

Tietjen-Moore Test for Outliers
Purpose:
Detection of Outliers 		The Tietjen-Moore test (Tietjen-Moore 1972) is used to detect multiple outliers in a univariate data set that follows an approximately normal distribution.

The Tietjen-Moore test is a generalization of the Grubbs' test to the case of multiple outliers. If testing for a single outlier, the Tietjen-Moore test is equivalent to the Grubbs' test.

It is important to note that the Tietjen-Moore test requires that the suspected number of outliers be specified exactly. If this is not known, it is recommended that the generalized extreme studentized deviate test be used instead (this test only requires an upper bound on the number of suspected outliers).

Definition The Tietjen-Moore test is defined for the hypothesis:

H0: There are no outliers in the data set
Ha: There are exactly k outliers in the data set
Test Statistic: Sort the n data points from smallest to the largest so that yi denotes the ith largest data value.

The test statistic for the k largest points is

    \( L_{k} = \frac{\sum_{i=1}^{n-k}{(y_{i} - \bar{y}_{k})^{2}}} {\sum_{i=1}^{n}{(y_{i} - \bar{y})^{2}}} \)

with \(\bar{y}\) denoting the sample mean for the full sample and \(\bar{y}_{k}\) denoting the sample mean with the largest k points removed.

The test statistic for the k smallest points is

    \( L_{k} = \frac{\sum_{i=k+1}^{n}{(y_{i} - \bar{y}_{k})^{2}}} {\sum_{i=1}^{n}{(y_{i} - \bar{y})^{2}}} \)

with \(\bar{y}\) denoting the sample mean for the full sample and \(\bar{y}_{k}\) denoting the sample mean with the smallest k points removed.

To test for outliers in both tails, compute the absolute residuals

    \( r_{i} = |y_{i} - \bar{y}| \)

and then let zi denote the yi values sorted by their absolute residuals in ascending order. The test statistic for this case is

    \( E_{k} = \frac{\sum_{i=1}^{n-k}{(z_{i} - \bar{z}_{k})^{2}}} {\sum_{i=1}^{n}{(z_{i} - \bar{z})^{2}}} \)

with \(\bar{z}\) denoting the sample mean for the full data set and \(\bar{z}_{k}\) denoting the sample mean with the largest k points removed.

Significance Level: α
Critical Region: The critical region for the Tietjen-Moore test is determined by simulation. The simulation is performed by generating a standard normal random sample of size n and computing the Tietjen-Moore test statistic. Typically, 10,000 random samples are used. The value of the Tietjen-Moore statistic obtained from the data is compared to this reference distribution.

The value of the test statistic is between zero and one. If there are no outliers in the data, the test statistic is close to 1. If there are outliers in the data, the test statistic will be closer to zero. Thus, the test is always a lower, one-tailed test regardless of which test statisic is used, Lk or Ek.

Sample Output The Tietjen-Moore paper gives the following 15 observations of vertical semi-diameters of the planet Venus (this example originally appeared in Grubbs' 1950 paper):
    -1.40 -0.44 -0.30 -0.24 -0.22 -0.13 -0.05 0.06 0.10 0.18 0.20 0.39 0.48 0.63 1.01
As a first step, a normal probability plot was generated.

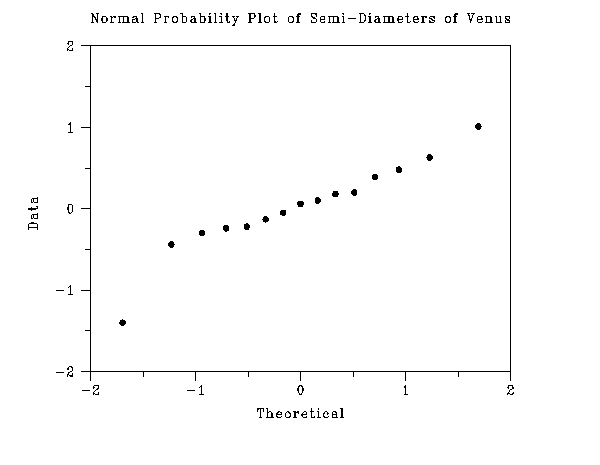
    Normal Probability Plot of Data

This plot indicates that the normality assumption is reasonable. The minimum value appears to be an outlier. To a lesser extent, the maximum value may also be an outlier. The Tietjen-Moore test of the two most extreme points (-1.40 and 1.01) is shown below. 

 
      H0:  there are no outliers in the data
      Ha:  the two most extreme points are outliers

      Test statistic:  Ek = 0.292
      Significance level:  α = 0.05
      Critical value for lower tail:  0.317
      Critical region:  Reject H0 if Ek < 0.317
The Tietjen-Moore test is a lower, one-tailed test, so we reject the null hypothesis that there are no outliers when the value of the test statistic is less than the critical value. For our example, the null hypothesis is rejected at the 0.05 level of significance and we conclude that the two most extreme points are outliers.
Questions The Tietjen-Moore test can be used to answer the following question:
  1. Does the data set contain k outliers?
Importance Many statistical techniques are sensitive to the presence of outliers. For example, simple calculations of the mean and standard deviation may be distorted by a single grossly inaccurate data point.

Checking for outliers should be a routine part of any data analysis. Potential outliers should be examined to see if they are possibly erroneous. If the data point is in error, it should be corrected if possible and deleted if it is not possible. If there is no reason to believe that the outlying point is in error, it should not be deleted without careful consideration. However, the use of more robust techniques may be warranted. Robust techniques will often downweight the effect of outlying points without deleting them.

Related Techniques Several graphical techniques can, and should, be used to help detect outliers. A simple normal probability plot, run sequence plot, a box plot, or a histogram should show any obviously outlying points. In addition to showing potential outliers, several of these graphics also help assess whether the data follow an approximately normal distribution.
Software Some general purpose statistical software programs support the Tietjen-Moore test. Both Dataplot code and R code can be used to generate the analyses in this section. These scripts use the TIETMOO1.DAT data file.
Home Tools & Aids Search Handbook Previous Page Next Page