1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.6. Probability Distributions

1.3.6.4.

Location and Scale Parameters

Normal PDF

A probability distribution is characterized by location and scale parameters. Location and scale parameters are typically used in modeling applications.

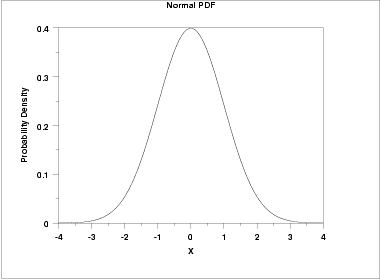
For example, the following graph is the probability density function for the standard normal distribution, which has the location parameter equal to zero and scale parameter equal to one.

Location Parameter

The next plot shows the probability density function for a normal distribution with a location parameter of 10 and a scale parameter of 1.

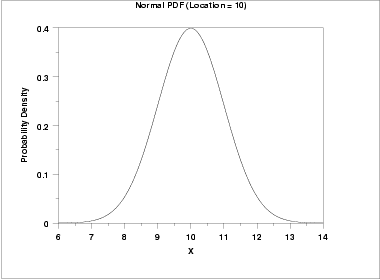
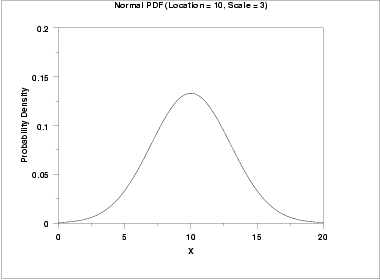
The effect of the location parameter is to translate the graph, relative to the standard normal distribution, 10 units to the right on the horizontal axis. A location parameter of -10 would have shifted the graph 10 units to the left on the horizontal axis.

That is, a location parameter simply shifts the graph left or right on the horizontal axis.

Scale Parameter

The next plot has a scale parameter of 3 (and a location parameter of zero). The effect of the scale parameter is to stretch out the graph. The maximum y value is approximately 0.13 as opposed 0.4 in the previous graphs. The y value, i.e., the vertical axis value, approaches zero at about (+/-) 9 as opposed to (+/-) 3 with the first graph.

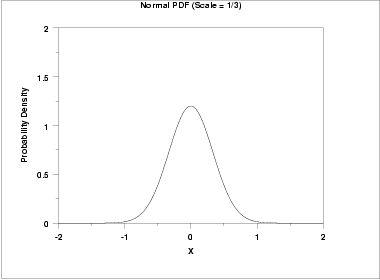
In contrast, the next graph has a scale parameter of 1/3 (=0.333). The effect of this scale parameter is to squeeze the pdf. That is, the maximum y value is approximately 1.2 as opposed to 0.4 and the y value is near zero at (+/-) 1 as opposed to (+/-) 3.

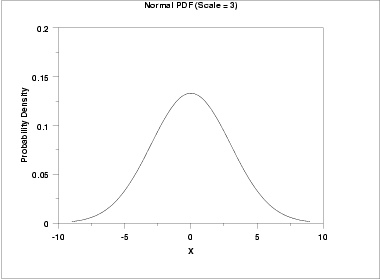
The effect of a scale parameter greater than one is to stretch the pdf. The greater the magnitude, the greater the stretching. The effect of a scale parameter less than one is to compress the pdf. The compressing approaches a spike as the scale parameter goes to zero. A scale parameter of 1 leaves the pdf unchanged (if the scale parameter is 1 to begin with) and non-positive scale parameters are not allowed.

Location and Scale Together

The following graph shows the effect of both a location and a scale parameter. The plot has been shifted right 10 units and stretched by a factor of 3.

Standard Form

The standard form of any distribution is the form that has location parameter zero and scale parameter one.

It is common in statistical software packages to only compute the standard form of the distribution. There are formulas for converting from the standard form to the form with other location and scale parameters. These formulas are independent of the particular probability distribution.

Formulas for Location and Scale Based on the Standard Form

The following are the formulas for computing various probability functions based on the standard form of the distribution. The parameter a refers to the location parameter and the parameter b refers to the scale parameter. Shape parameters are not included.

Cumulative Distribution Function	F(x;a,b) = F((x-a)/b;0,1)
Probability Density Function	f(x;a,b) = (1/b)f((x-a)/b;0,1)
Percent Point Function	G(α;a,b) = a + bG(α;0,1)
Hazard Function	h(x;a,b) = (1/b)h((x-a)/b;0,1)
Cumulative Hazard Function	H(x;a,b) = H((x-a)/b;0,1)
Survival Function	S(x;a,b) = S((x-a)/b;0,1)
Inverse Survival Function	Z(α;a,b) = a + bZ(α;0,1)
Random Numbers	Y(a,b) = a + bY(0,1)

Relationship to Mean and Standard Deviation

For the normal distribution, the location and scale parameters correspond to the mean and standard deviation, respectively. However, this is not necessarily true for other distributions. In fact, it is not true for most distributions.