1. Exploratory Data Analysis
1.3. EDA Techniques
1.3.6. Probability Distributions
1.3.6.6. Gallery of Distributions

1.3.6.6.18.

Binomial Distribution

Probability Mass Function

The binomial distribution is used when there are exactly two mutually exclusive outcomes of a trial. These outcomes are appropriately labeled "success" and "failure". The binomial distribution is used to obtain the probability of observing x successes in N trials, with the probability of success on a single trial denoted by p. The binomial distribution assumes that p is fixed for all trials.

The formula for the binomial probability mass function is

$P(x;p,n)=\left(\begin{array}{c}n\\ x\end{array}\right)(p{)}^x(1-p{)}^{(n-x)}\text{for }x=0,1,2,\cdots ,n$

where

$\left(\begin{array}{c}n\\ x\end{array}\right)=\frac{n!}{x!(n-x)!}$

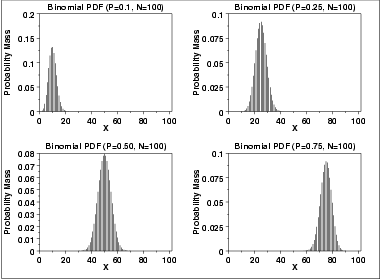
The following is the plot of the binomial probability density function for four values of p and n = 100.

Cumulative Distribution Function

The formula for the binomial cumulative probability function is

$F(x;p,n)=\sum _{i=0}^x\left(\begin{array}{c}n\\ i\end{array}\right)(p{)}^i(1-p{)}^{(n-i)}$

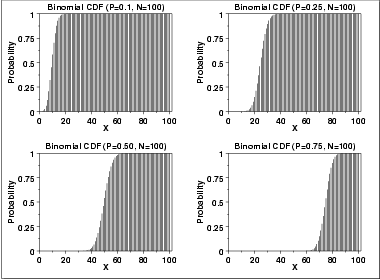
The following is the plot of the binomial cumulative distribution function with the same values of p as the pdf plots above.

Percent Point Function

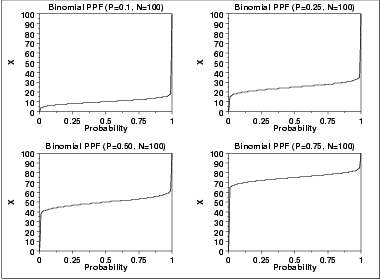
The binomial percent point function does not exist in simple closed form. It is computed numerically. Note that because this is a discrete distribution that is only defined for integer values of x, the percent point function is not smooth in the way the percent point function typically is for a continuous distribution.

The following is the plot of the binomial percent point function with the same values of p as the pdf plots above.

Common Statistics

Mean	np
Mode	p(n + 1) - 1 ≤ x ≤ p(n + 1)
Range	0 to n
Standard Deviation	$\sqrt{np(1-p)}$
Coefficient of Variation	$\sqrt{\frac{(1-p)}{np}}$
Skewness	$\frac{(1-2p)}{\sqrt{np(1-p)}}$
Kurtosis	$3-\frac{6}{n}+\frac{1}{np(1-p)}$

Comments

The binomial distribution is probably the most commonly used discrete distribution.

Parameter Estimation

The maximum likelihood estimator of p (for fixed n) is

$\tilde{p}=\frac{x}{n}$

Software

Most general purpose statistical software programs support at least some of the probability functions for the binomial distribution.