Next Page Previous Page Home Tools & Aids Search Handbook
1. Exploratory Data Analysis
1.4. EDA Case Studies
1.4.2. Case Studies
1.4.2.10. Ceramic Strength

1.4.2.10.3.

Analysis of the Batch Effect
Batch is a Nuisance Factor The two nuisance factors in this experiment are the batch number and the lab. There are two batches and eight labs. Ideally, these factors will have minimal effect on the response variable.

We will investigate the batch factor first.

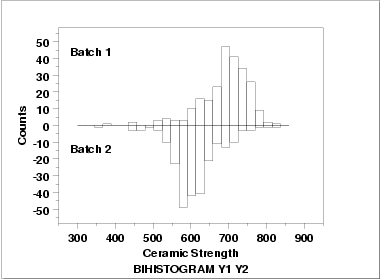
Bihistogram Bihistogram

This bihistogram shows the following.

  1. There does appear to be a batch effect.

  2. The batch 1 responses are centered at 700 while the batch 2 responses are centered at 625. That is, the batch effect is approximately 75 units.

  3. The variability is comparable for the 2 batches.

  4. Batch 1 has some skewness in the lower tail. Batch 2 has some skewness in the center of the distribution, but not as much in the tails compared to batch 1.

  5. Both batches have a few low-lying points.

Although we could stop with the bihistogram, we will show a few other commonly used two-sample graphical techniques for comparison.

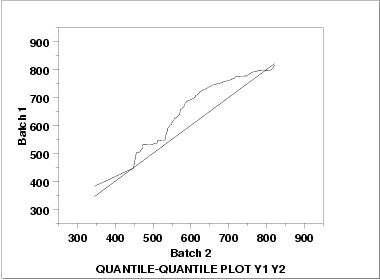
Quantile-Quantile Plot Quantile-Quantile Plot

This q-q plot shows the following.

  1. Except for a few points in the right tail, the batch 1 values have higher quantiles than the batch 2 values. This implies that batch 1 has a greater location value than batch 2.

  2. The q-q plot is not linear. This implies that the difference between the batches is not explained simply by a shift in location. That is, the variation and/or skewness varies as well. From the bihistogram, it appears that the skewness in batch 2 is the most likely explanation for the non-linearity in the q-q plot.
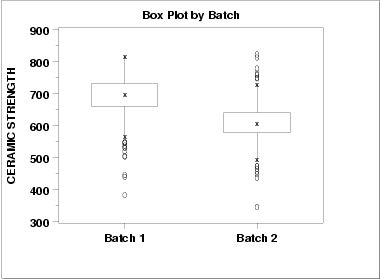
Box Plot Box Plot

This box plot shows the following.

  1. The median for batch 1 is approximately 700 while the median for batch 2 is approximately 600.

  2. The spread is reasonably similar for both batches, maybe slightly larger for batch 1.

  3. Both batches have a number of outliers on the low side. Batch 2 also has a few outliers on the high side. Box plots are a particularly effective method for identifying the presence of outliers.
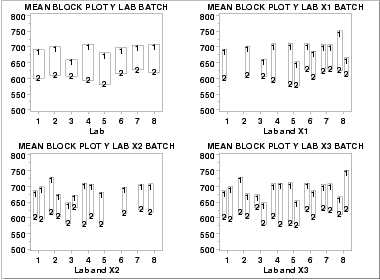
Block Plots A block plot is generated for each of the eight labs, with "1" and "2" denoting the batch numbers. In the first plot, we do not include any of the primary factors. The next 3 block plots include one of the primary factors. Note that each of the 3 primary factors (table speed = X1, down feed rate = X2, wheel grit size = X3) has 2 levels. With 8 labs and 2 levels for the primary factor, we would expect 16 separate blocks on these plots. The fact that some of these blocks are missing indicates that some of the combinations of lab and primary factor are empty.

Block Plots

These block plots show the following.

  1. The mean for batch 1 is greater than the mean for batch 2 in all of the cases above. This is strong evidence that the batch effect is real and consistent across labs and primary factors.
Quantitative Techniques We can confirm some of the conclusions drawn from the above graphics by using quantitative techniques. The F-test can be used to test whether or not the variances from the two batches are equal and the two sample t-test can be used to test whether or not the means from the two batches are equal. Summary statistics for each batch are shown below. 

Batch 1:
    NUMBER OF OBSERVATIONS =  240
    MEAN                   =  688.9987
    STANDARD DEVIATION     =   65.5491
    VARIANCE               = 4296.6845 
 
Batch 2:
    NUMBER OF OBSERVATIONS =  240
    MEAN                   =  611.1559
    STANDARD DEVIATION     =   61.8543
    VARIANCE               = 3825.9544
F-Test The two-sided F-test indicates that the variances for the two batches are not significantly different at the 5 % level. 

H0:  σ12 = σ22 
Ha:  σ12 ≠ σ22

Test statistic:  F = 1.123 
Numerator degrees of freedom:  ν1 = 239
Denominator degrees of freedom:  ν2 = 239
Significance level:  α = 0.05
Critical values:  F1-α/2,ν1,ν2 = 0.845
                  Fα/2,ν1,ν2 = 1.289
Critical region:  Reject H0 if F < 0.845 or F > 1.289
Two Sample t-Test Since the F-test indicates that the two batch variances are equal, we can pool the variances for the two-sided, two-sample t-test to compare batch means. 

H0:  μ1 = μ2
Ha:  μ1 ≠ μ2

Test statistic:  T = 13.3806 
Pooled standard deviation:  sp = 63.7285
Degrees of freedom:  ν = 478
Significance level:  α = 0.05
Critical value:  t1-α/2,ν = 1.965
Critical region: Reject H0 if |T| > 1.965
The t-test indicates that the mean for batch 1 is larger than the mean for batch 2 at the 5 % significance level.
Conclusions We can draw the following conclusions from the above analysis.
  1. There is in fact a significant batch effect. This batch effect is consistent across labs and primary factors.

  2. The magnitude of the difference is on the order of 75 to 100 (with batch 2 being smaller than batch 1). The standard deviations do not appear to be significantly different.

  3. There is some skewness in the batches.

This batch effect was completely unexpected by the scientific investigators in this study.

Note that although the quantitative techniques support the conclusions of unequal means and equal standard deviations, they do not show the more subtle features of the data such as the presence of outliers and the skewness of the batch 2 data.

Home Tools & Aids Search Handbook Previous Page Next Page