2.5.3.3.3. Bias with sparse data

Strategy for dealing with limited data

The purpose of this discussion is to outline methods for dealing with biases that may be real but which cannot be estimated reliably because of the sparsity of the data. For example, a test between two, of many possible, configurations of the measurement process cannot produce a reliable enough estimate of bias to permit a correction, but it can reveal problems with the measurement process. The strategy for a significant bias is to apply a 'zero' correction. The type A uncertainty component is the standard deviation of the correction, and the calculation depends on whether the bias is

• inconsistent
• consistent

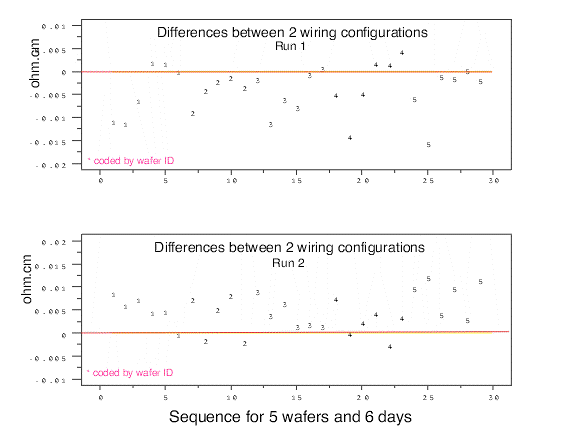
Example of differences among wiring settings

An example is given of a study of wiring settings for a single gauge. The gauge, a 4-point probe for measuring resistivity of silicon wafers, can be wired in several ways. Because it was not possible to test all wiring configurations during the gauge study, measurements were made in only two configurations as a way of identifying possible problems.

Data on wiring configurations

Measurements were made on six wafers over six days (except for 5 measurements on wafer 39) with probe #2062 wired in two configurations. This sequence of measurements was repeated after about a month resulting in two runs. A database of differences between measurements in the two configurations on the same day are analyzed for significance.

Run software macro for making plotting differences between the 2 wiring configurations

A plot of the differences between the 2 configurations shows that the differences for run 1 are, for the most part, < zero, and the differences for run 2 are > zero. The following Dataplot commands produce the plot:

dimension 30 columns
skip 25
read mpc536.dat wafer day probe d1 d2
let n = count probe
let t = sequence 1 1 n
let zero = 0 for i = 1 1 n
lines dotted blank blank
characters blank 1 2
x1label = DIFFERENCES BETWEEN 2 WIRING CONFIGURATIONS 
x2label SEQUENCE BY WAFER AND DAY
plot zero d1 d2 vs t

Statistical test for difference between 2 configurations	A t-statistic is used as an approximate test where we are assuming the differences are approximately normal. The average difference and standard deviation of the difference are required for this test. If \( \displaystyle \large{ t = \left| \frac{\sqrt{N}}{s_{diff}} Avg_{diff} \right| > 2 } \) the difference between the two configurations is statistically significant. The average and standard deviation computed from the N = 29 differences in each run from the table above are shown along with corresponding t-values which confirm that the differences are significant, but in opposite directions, for both runs. Average differences between wiring configurations Run Probe Average Std dev N t 1 2062 - 0.00383 0.00514 29 - 4.0 2 2062 + 0.00489 0.00400 29 + 6.6
Run software macro for making t-test	The following Dataplot commands let dff = n-1 let avgrun1 = average d1 let avgrun2 = average d2 let sdrun1 = standard deviation d1 let sdrun2 = standard deviation d2 let t1 = ((n-1)**.5)*avgrun1/sdrun1 let t2 = ((n-1)**.5)*avgrun2/sdrun2 print avgrun1 sdrun1 t1 print avgrun2 sdrun2 t2 let tcrit=tppf(.975,dff) reproduce the statistical tests in the table. PARAMETERS AND CONSTANTS-- AVGRUN1 -- -0.3834483E-02 SDRUN1 -- 0.5145197E-02 T1 -- -0.4013319E+01 PARAMETERS AND CONSTANTS-- AVGRUN2 -- 0.4886207E-02 SDRUN2 -- 0.4004259E-02 T2 -- 0.6571260E+01
Case of inconsistent bias	The data reveal a significant wiring bias for both runs that changes direction between runs. Because of this inconsistency, a 'zero' correction is applied to the results, and the type A uncertainty is taken to be \( \displaystyle \large{ s_{correction} = \frac{1}{\sqrt{3}} MaxBias } \) For this study, the type A uncertainty for wiring bias is \( \displaystyle \large{ s_{correction} = \frac{1}{\sqrt{3}} 0.00489 \,\, \mbox{ohm.cm} = 0.0028 \,\, \mbox{ohm.cm} } \)
Case of consistent bias	Even if the bias is consistent over time, a 'zero' correction is applied to the results, and for a single run, the estimated standard deviation of the correction is \( \displaystyle \large{ s_{correction} = \frac{1}{\sqrt{N}} s_{diff} } \) For two runs (1 and 2), the estimated standard deviation of the correction is \( \displaystyle \large{ s_{correction} = \frac{1}{\sqrt{2N}} \sqrt{ s_{{diff}_1}^2 + s_{{diff}_2}^2 } } \)