6. Process or Product Monitoring and Control
6.3. Univariate and Multivariate Control Charts
6.3.2. What are Variables Control Charts?

6.3.2.4.

EWMA Control Charts

EWMA statistic

The Exponentially Weighted Moving Average (EWMA) is a statistic for monitoring the process that averages the data in a way that gives less and less weight to data as they are further removed in time.

Comparison of Shewhart control chart and EWMA control chart techniques

For the Shewhart chart control technique, the decision regarding the state of control of the process at any time, t, depends solely on the most recent measurement from the process and, of course, the degree of 'trueness' of the estimates of the control limits from historical data. For the EWMA control technique, the decision depends on the EWMA statistic, which is an exponentially weighted average of all prior data, including the most recent measurement.

By the choice of weighting factor, , the EWMA control procedure can be made sensitive to a small or gradual drift in the process, whereas the Shewhart control procedure can only react when the last data point is outside a control limit.

Definition of EWMA

The statistic that is calculated is:

EWMA_t = Y_t + ( 1- ) EWMA_t-1    for t = 1, 2, ..., n.

where

• EWMA₀ is the mean of historical data (target)
• Y_t is the observation at time t
• n is the number of observations to be monitored including EWMA₀
• 0 < 1 is a constant that determines the depth of memory of the EWMA.

The equation is due to Roberts (1959).

Choice of weighting factor

The parameter determines the rate at which 'older' data enter into the calculation of the EWMA statistic. A value of = 1 implies that only the most recent measurement influences the EWMA (degrades to Shewhart chart). Thus, a large value of = 1 gives more weight to recent data and less weight to older data; a small value of gives more weight to older data. The value of is usually set between 0.2 and 0.3 (Hunter) although this choice is somewhat arbitrary. Lucas and Saccucci (1990) give tables that help the user select .

Variance of EWMA statistic

The estimated variance of the EWMA statistic is approximately

s²_ewma = (/(2- )) s²

when t is not small, where s is the standard deviation calculated from the historical data.

Definition of control limits for EWMA

The center line for the control chart is the target value or EWMA₀. The control limits are:

UCL = EWMA₀ + ks_ewma
LCL = EWMA₀ - ks_ewma

where the factor k is either set equal 3 or chosen using the Lucas and Saccucci (1990) tables. The data are assumed to be independent and these tables also assume a normal population.

As with all control procedures, the EWMA procedure depends on a database of measurements that are truly representative of the process. Once the mean value and standard deviation have been calculated from this database, the process can enter the monitoring stage, provided the process was in control when the data were collected. If not, then the usual Phase 1 work would have to be completed first.

Example of calculation of parameters for an EWMA control chart

To illustrate the construction of an EWMA control chart, consider a process with the following parameters calculated from historical data:

EWMA₀ = 50
s = 2.0539

with chosen to be 0.3 so that / (2-) = .3 / 1.7 = 0.1765 and the square root = 0.4201. The control limits are given by

UCL = 50 + 3 (0.4201)(2.0539) = 52.5884
LCL = 50 - 3 (0.4201) (2.0539) = 47.4115

Sample data

Consider the following data consisting of 20 points where 1 - 10 are on the top row from left to right and 11-20 are on the bottom row from left to right:

  52.0 47.0 53.0 49.3 50.1 47.0
  51.0 50.1 51.2 50.5 49.6 47.6
  49.9 51.3 47.8 51.2 52.6 52.4
  53.6 52.1

EWMA statistics for sample data

These data represent control measurements from the process which is to be monitored using the EWMA control chart technique. The corresponding EWMA statistics that are computed from this data set are:

  50.00 50.60 49.52 50.56 50.18
  50.16 49.12 49.75 49.85 50.26
  50.33 50.11 49.36 49.52 50.05
  49.34 49.92 50.73 51.23 51.94

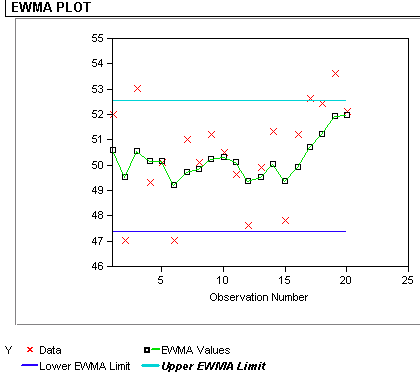
Sample EWMA plot

The control chart is given below.

Interpretation of EWMA control chart

The red dots are the raw data; the jagged line is the EWMA statistic over time. The chart tells us that the process is in control because all EWMAt lie between the control limits. However, there seems to be a trend upwards for the last 5 periods.