4.3. Data Collection for Process Modeling
4.3.4. |
I've heard some people refer to "optimal" designs, shouldn't I use those? |
- Limited maximum number of runs:
User constraints in budget and time may dictate a maximum allowable number of runs that is too small or too "irregular" (e.g., "13") to be accommodated by classical designs--even fractional factorial designs.
- Impossible factor combinations:
The user may have some factor combinations that are impossible to run. Such combinations may at times be specified (to maintain balance and orthogonality) as part of a recommeded classical design. If the user simply omits this impossible run from the design, the net effect may be a reduction in the quality and optimaltiy of the classical design.
- Too many levels:
The number of factors and/or the number of levels of some factors intended for use may not be included in tabulations of classical designs.
- Complicated underlying model:
The user may be assuming an underlying model that is too complicated (or too non-linear), so that classical designs would be inappropriate.
The previous section's list of design criteria (capability for the primary model, capability for the alternate model, minimum variation of estimated coefficients, etc.) is a good passive target to aim for in terms of desirable design properties, but provides little help in terms of an active formal construction methodology for generating a design.
| D-optimal designs: | minimize the generalized variance of the parameter estimators. |
| A-optimal designs: | minimize the average variance of the parameter estimators. |
| G-optimal designs: | minimize the maximum variance of the predicted values. |
| V-optimal designs: | minimize the average variance of the predicted values. |
All optimal designs are model-dependent, and so the quality of the final engineering conclusions that result from the ensuing design, data, and analysis is dependent on the correctness of the analyst's assumed model. For example, if the responses from a particular process are actually being drawn from a cubic model and the analyst assumes a linear model and uses the corresponding optimal design to generate data and perform the data analysis, then the final engineering conclusions will be flawed and invalid. Hence one price for obtaining an in-hand generated design is the designation of a model. All optimal designs need a model; without a model, the optimal design-generation methodology cannot be used, and general design principles must be reverted to.
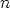 points from a larger superset of
candidate points. The user must specify this candidate set of
points. Most commonly, the superset of candidate points is the
full factorial design over a fine-enough grid of the factor
space with which the analyst is comfortable. If the grid
is too fine, and the resulting superset overly large, then
the optimal design methodology may prove computationally
challenging.
points from a larger superset of
candidate points. The user must specify this candidate set of
points. Most commonly, the superset of candidate points is the
full factorial design over a fine-enough grid of the factor
space with which the analyst is comfortable. If the grid
is too fine, and the resulting superset overly large, then
the optimal design methodology may prove computationally
challenging.
For further details about optimal designs, the analyst is referred to Montgomery (2001).

