4. Process Modeling
4.8. Some Useful Functions for Process Modeling
4.8.1. Univariate Functions
4.8.1.2. Rational Functions

4.8.1.2.4.

Quadratic / Linear Rational Function

Function:	\( \displaystyle f(x) = \frac{\beta_0 + \beta_1x + \beta_2x^2}{1 + \beta_3x}, \ \ \beta_2 \neq 0, \ \beta_3 \neq 0 \)
Function Family:	Rational
Statistical Type:	Nonlinear
Domain:	\( \displaystyle \left(-\infty, \ -\frac{1}{\beta_3}\right) \ \cup \ \left(-\frac{1}{\beta_3}, \ \infty\right) \)
Range:	\( \displaystyle \left\{ \begin{array}{lll} (-\infty, \, \infty) & \mbox{for} & \beta_2^2-(\beta_1-\beta_0\beta_3)\beta_2\beta_3 \leq 0 \\ & & \\ (-\infty, \, f_{max}] \, \cup \, [f_{min}, \, \infty) & \mbox{for} & \beta_2^2-(\beta_1-\beta_0\beta_3)\beta_2\beta_3 > 0 \end{array} \right. \) with \( \displaystyle f_{min} = \max \left[ f \left( \frac{-\beta_2-\sqrt{\beta_2^2-\beta_0\beta_3}}{\beta_2\beta_3} \right), \ f \left( \frac{-\beta_2+\sqrt{\beta_2^2-\beta_0\beta_3}}{\beta_2\beta_3} \right) \right] \) and \( \displaystyle f_{max} = \min \left[ f \left( \frac{-\beta_2-\sqrt{\beta_2^2-\beta_0\beta_3}}{\beta_2\beta_3} \right), \ f \left( \frac{-\beta_2+\sqrt{\beta_2^2-\beta_0\beta_3}}{\beta_2\beta_3} \right) \right] \)
Special Features:	Vertical asymptote at: \( \displaystyle x = -\frac{1}{\beta_3} \)
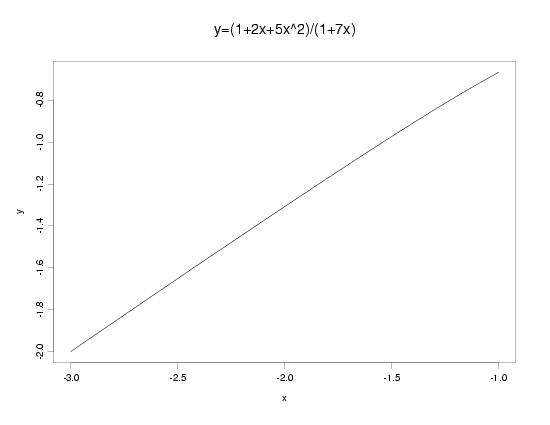
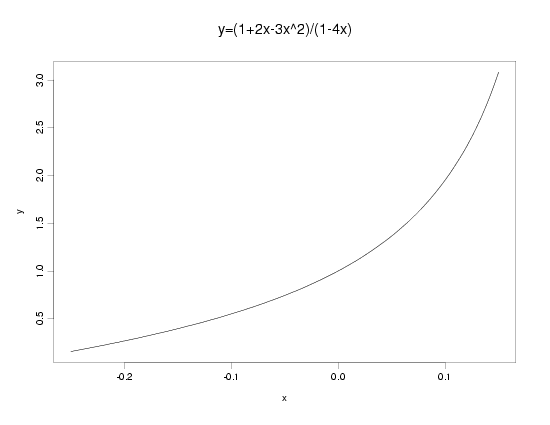
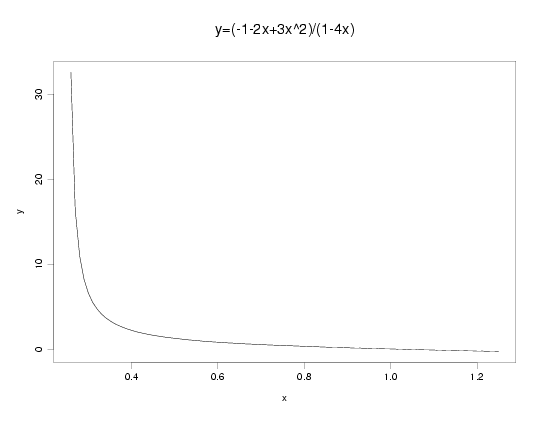
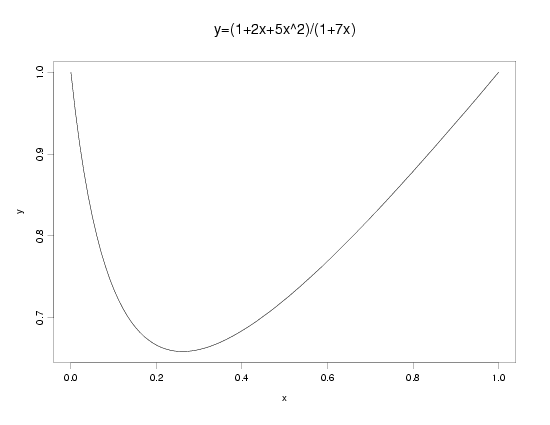
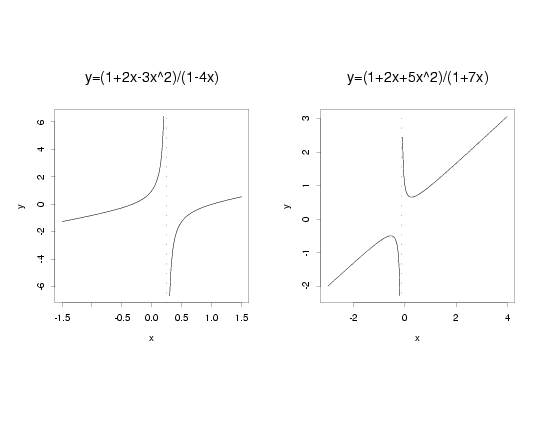
Additional Examples: