4. Process Modeling
4.8. Some Useful Functions for Process Modeling
4.8.1. Univariate Functions
4.8.1.2. Rational Functions

4.8.1.2.8.

Linear / Cubic Rational Function

Function:	${\displaystyle f(x)=\frac{{\beta }_0+{\beta }_{1}x}{1+{\beta }_{2}x+{\beta }_3{x}^2+{\beta }_4{x}^3},{\beta }_1\ne 0,{\beta }_4\ne 0}$
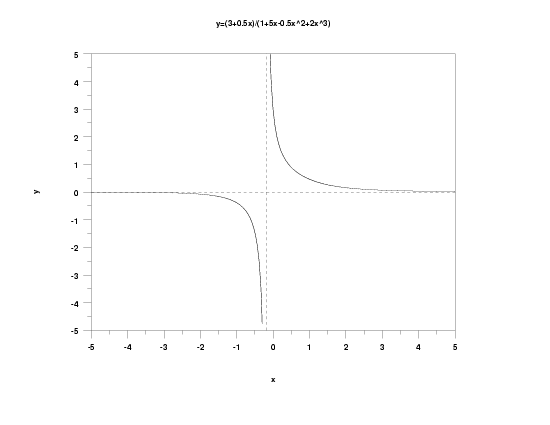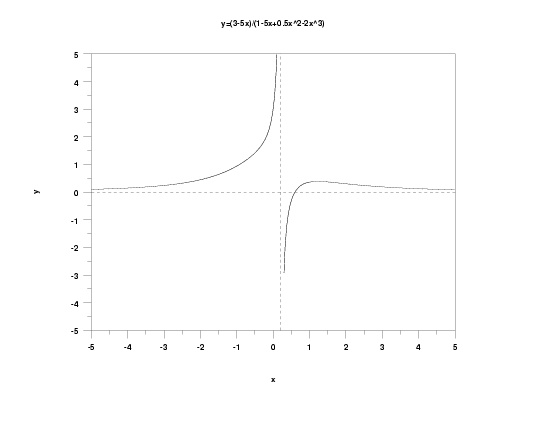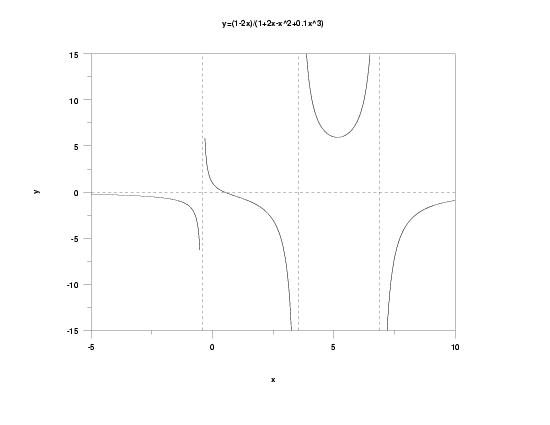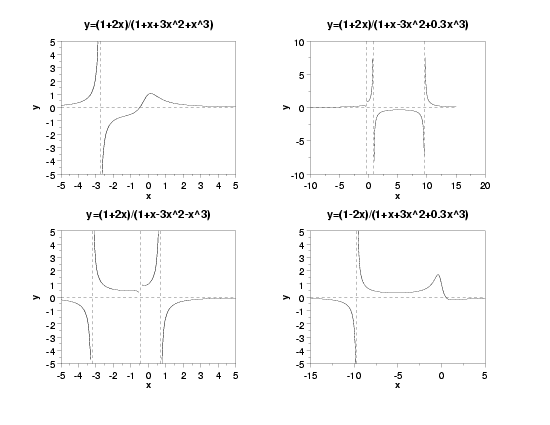
Function Family:	Rational
Statistical Type:	Nonlinear
Domain:	${\displaystyle (-\mathrm{\infty },\mathrm{\infty })}$ with undefined points at the roots of ${\displaystyle 1+{\beta }_{2}x+{\beta }_3{x}^2+{\beta }_4{x}^3}$ There will be 1, 2, or 3 roots, depending on the particular values of the parameters. Explicit solutions for the roots of a cubic polynomial are complicated and are not given here. Many mathematical and statistical software programs can determine the roots of a polynomial equation numerically, and it is recommended that you use one of these programs if you need to know where these roots occur.
Range:	${\displaystyle (-\mathrm{\infty },\mathrm{\infty })}$ with the possible exception that zero may be excluded.
Special Features:	Horizontal asymptote at: ${\displaystyle y=0}$ and vertical asymptotes at the roots of ${\displaystyle 1+{\beta }_{2}x+{\beta }_3{x}^2+{\beta }_4{x}^3}$ There will be 1, 2, or 3 roots, depending on the particular values of the parameters. Explicit solutions for the roots of a cubic polynomial are complicated and are not given here. Many mathematical and statistical software programs can determine the roots of a polynomial equation numerically, and it is recommended that you use one of these programs if you need to know where these roots occur.
Additional Examples: