5. Process Improvement
5.3. Choosing and running an experimental design
5.3.3. How do you select an experimental design?
5.3.3.2. Fractional factorial designs

5.3.3.2.4.

Design resolution: A measure of merit

Generating relation and diagram for the 2^8-3 fractional factorial design
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

"Defining relation "for a factorial design

Definition of "Resolution"
 
 
 
 

Notation for resolution (roman numerals)
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

Resolution and confounding
 
 
 
 

 

We have considered the 2^3-1 design in the previous section, and seen that its generating relation written in '‘I =...'’form is { I = + 123 }. Now consider the one-eighth fraction of a 2⁸ design, namely the 2^8-3 fractional factorial design. Using a diagram similar to Figure 3.5, we are given the following: 
 

FIGURE 3.6  Specifications for a 2^8-3 Design

Figure 3.6 tells us that a 2^8-3 design has thirty-two runs, not including centerpoint runs, and up to eight factors. There are three generating relations. In order to construct the design, we do the following: 

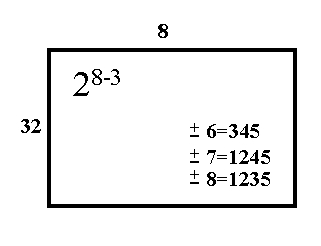
(1)  Write down a full factorial for 8-3 = 5 factors; that is, a 2⁵ full factorial design. Such a design has 2⁵ = 32 rows. 
(2)  Add a sixth column to the design table for factor 6, using 6 = 345 (or 6 = -345) to manufacture it (i.e. using the column multiplication we discussed above). 
(3)  Do likewise for factor 7 and for factor 8, using the appropriate generating relations given in Figure 3.6. 

We note further that the generating relations, written in ‘I = ...’ form, for the 2^8-3 is 

{ I = ± 3456; I = ± 12457; I = ± 12358 }.

This collection of generating relations for a factorial design is called a defining relation. There are three ‘words’ in the defining relation for the 2^8-3 design. The length of the shortest word in the defining relation is called the resolution of the design. Resolution describes the degree to which estimated main effects are aliased (or confounded) with estimated 2-level interactions, 3-level interactions, etc

The length of the shortest word in the defining relation for the 2^8-3 design is four. This is written in Roman numeral script, and sub-scripted as 2_IV^8-3. Note that the 2^3-1 design has one word: ‘I = ±123’ in its defining relation, and so has resolution three; that is, we may write 2_III^3-1. 

Now Figure 3.6 may be completed by writing it as: 

FIGURE 3.7  Specifications for a 2^8-3, Showing Resolution ‘IV’

The design resolution tells us how badly the design is confounded. Previously, in the 2^3-1 design, we saw the main effects were confounded with two-factor interactions. However, main effects were not confounded with other main effects. So, at worst, we have 3=12, or 2=13, etc., but we do not have 1=1, or 2=2, etc. In fact, a resolution II design would be pretty useless for any purpose whatsoever! 

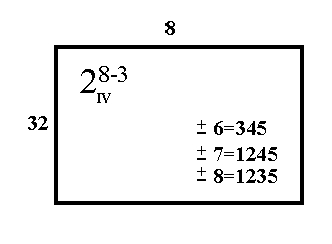
Similarly, in a resolution IV design, main effects are confounded with at worst three-factor interactions. We can see, in Figure 3.7, that 6=345. We also see that 36=45, 34=56, etc. (i.e. two-factor interactions are confounded with certain other two-factor interactions) etc.; but we never see the likes of  2=13, or 5=34, (main effects confounded with two-factor interactions). 

The complete confounding pattern, for confounding of up to two-factor interactions, arising from the design given in Figure 3.7 is 

34 = 56 = 78
35 = 46
36 = 45
37 = 48
38 = 47
57 = 68

Note that we have deliberately left out reference to three-factor interactions, and higher than three-factor interactions, because as we have said they are assumed negligible. (This may be a wrong assumption in some rare instances). 

If we are interested in estimating up to two of the two-factor interactions free of confounding with other two-factor interaction when running this design, we would assign those factors of interest to columns 1 or column 2. This type of consideration is often key in choosing and setting up a design. 

This means that a resolution IV design is ‘better’ than a resolution III design because we have a less severe confounding pattern in the ‘IV’ than in the ‘III’ situation; higher order interactions are usually assumed to be much less significant than low-order interactions. 

A higher resolution design for the same number of factors will, however, require more runs and so it is ‘worse’ than a lower-order design in that sense. 

Similarly, a resolution V design, main effects would be confounded with at worst four-factor interactions, and two factor interactions would be confounded with certain three-factor interactions. 

Example: The 2^8-3 design is of resolution IV, and requires 32 runs. The 2^8-2 design, also for eight factors, has resolution V, but requires 64 runs. 

The identifying relation for a design is not necessarily unique. An alternative relation that will generate a 2^8-3 design is { I = ± 1236; I = ± 1247; I = ± 23458 }. Diagramatically, this is 

 FIGURE 3.8  Another Way of Generating the 2^8-3 Design

 

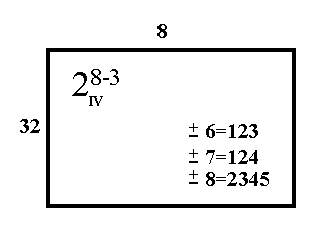
Commonly used design Resolutions 

Design Resolution Summary

The meaning of the most prevalent resolution levels is as follows: 

Resolution III Designs
Main effects are confounded or aliased with two-factor
interactions  and two-factor interactions are aliased with
each other. 
Resolution IV Designs 
No main effects are aliased  with two-factor interactions ,
but two-factor interactions are aliased with each other. 

Resolution V Designs
No main effect or two-factor interaction is aliased with any

     other main effect or two-factor interaction, but two-factor interactions are aliased with three-factor interactions