5. Process Improvement
5.3. Choosing an experimental design
5.3.3. How do you select an experimental design?
5.3.3.3. Full factorial designs

5.3.3.3.2.

Full factorial example

A Full Factorial Design Example

An example of a full factorial design with 3 factors

The following is an example of a full factorial design with 3 factors that also illustrates replication, randomization, and added center points.

Suppose that we wish to improve the yield of a polishing operation. The three inputs (factors) that are considered important to the operation are Speed (X₁), Feed (X₂), and Depth (X₃). We want to ascertain the relative importance of each of these factors on Yield (Y).

Speed, Feed and Depth can all be varied continuously along their respective scales, from a low to a high setting. Yield is observed to vary smoothly when progressive changes are made to the inputs. This leads us to believe that the ultimate response surface for Y will be smooth.

Table of factor level settings

TABLE 3.5  High (+1), Low (-1), and Standard (0) Settings for a Polishing Operation

	Low (-1)	Standard (0)	High (+1)	Units
Speed	16	20	24	rpm
Feed	0.001	0.003	0.005	cm/sec
Depth	0.01	0.015	0.02	cm/sec

Factor Combinations

Graphical representation of the factor level settings

We want to try various combinations of these settings so as to establish the best way to run the polisher. There are eight different ways of combining high and low settings of Speed, Feed, and Depth. These eight are shown at the corners of the following diagram.

FIGURE 3.2  A 2³ Two-level, Full Factorial Design; Factors X₁, X₂, X₃. (The arrows show the direction of increase of the factors.)

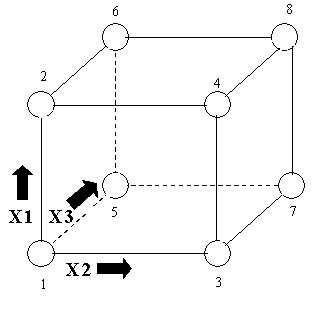
2³ implies 8 runs

Note that if we have k factors, each run at two levels, there will be 2^k different combinations of the levels. In the present case, k = 3 and 2³ = 8.

Full Model

Running the full complement of all possible factor combinations means that we can estimate all the main and interaction effects. There are three main effects, three two-factor interactions, and a three-factor interaction, all of which appear in the full model as follows:

\( \begin{array}{lcl} Y & = & \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}X_{3} + \\ & & \beta_{12}X_{1}X_{2} + \beta_{13}X_{1}X_{3} + \beta_{23}X_{2}X_{3} + \\ & & \beta_{123}X_{1}X_{2}X_{3} + \epsilon \end{array} \)

A full factorial design allows us to estimate all eight `beta' coefficients \( \{\beta_{0}, \ldots , \beta_{123} \} \).

Standard order

Coded variables in standard order

The numbering of the corners of the box in the last figure refers to a standard way of writing down the settings of an experiment called `standard order'. We see standard order displayed in the following tabular representation of the eight-cornered box. Note that the factor settings have been coded, replacing the low setting by -1 and the high setting by 1.

Factor settings in tabular form

TABLE 3.6  A 2³ Two-level, Full Factorial Design Table Showing Runs in `Standard Order'

	X1	X2	X3
1	-1	-1	-1
2	+1	-1	-1
3	-1	+1	-1
4	+1	+1	-1
5	-1	-1	+1
6	+1	-1	+1
7	-1	+1	+1
8	+1	+1	+1

Replication

Replication provides information on variability

Running the entire design more than once makes for easier data analysis because, for each run (i.e., `corner of the design box') we obtain an average value of the response as well as some idea about the dispersion (variability, consistency) of the response at that setting.

Homogeneity of variance

One of the usual analysis assumptions is that the response dispersion is uniform across the experimental space. The technical term is `homogeneity of variance'. Replication allows us to check this assumption and possibly find the setting combinations that give inconsistent yields, allowing us to avoid that area of the factor space.

Factor settings in standard order with replication

We now have constructed a design table for a two-level full factorial in three factors, replicated twice.

TABLE 3.7  The 2³ Full Factorial Replicated Twice and Presented in Standard Order

	Speed, X1	Feed, X2	Depth, X3
1	16, -1	.001, -1	.01, -1
2	24, +1	.001, -1	.01, -1
3	16, -1	.005, +1	.01, -1
4	24, +1	.005, +1	.01, -1
5	16, -1	.001, -1	.02, +1
6	24, +1	.001, -1	.02, +1
7	16, -1	.005, +1	.02, +1
8	24, +1	.005, +1	.02, +1
9	16, -1	.001, -1	.01, -1
10	24, +1	.001, -1	.01, -1
11	16, -1	.005, +1	.01, -1
12	24, +1	.005, +1	.01, -1
13	16, -1	.001, -1	.02, +1
14	24, +1	.001, -1	.02, +1
15	16, -1	.005, +1	.02, +1
16	24, +1	.005, +1	.02, +1

Randomization

No randomization and no center points

If we now ran the design as is, in the order shown, we would have two deficiencies, namely:

1. no randomization, and
2. no center points.

Randomization provides protection against extraneous factors affecting the results

The more freely one can randomize experimental runs, the more insurance one has against extraneous factors possibly affecting the results, and hence perhaps wasting our experimental time and effort. For example, consider the `Depth' column: the settings of Depth, in standard order, follow a `four low, four high, four low, four high' pattern.

Suppose now that four settings are run in the day and four at night, and that (unknown to the experimenter) ambient temperature in the polishing shop affects Yield. We would run the experiment over two days and two nights and conclude that Depth influenced Yield, when in fact ambient temperature was the significant influence. So the moral is: Randomize experimental runs as much as possible.

Table of factor settings in randomized order

Here's the design matrix again with the rows randomized. The old standard order column is also shown for comparison and for re-sorting, if desired, after the runs are in.

TABLE 3.8  The 2³ Full Factorial Replicated Twice with Random Run Order Indicated

Random Order	Standard Order	X1	X2	X3
1	5	-1	-1	+1
2	15	-1	+1	+1
3	9	-1	-1	-1
4	7	-1	+1	+1
5	3	-1	+1	-1
6	12	+1	+1	-1
7	6	+1	-1	+1
8	4	+1	+1	-1
9	2	+1	-1	-1
10	13	-1	-1	+1
11	8	+1	+1	+1
12	16	+1	+1	+1
13	1	-1	-1	-1
14	14	+1	-1	+1
15	11	-1	+1	-1
16	10	+1	-1	-1

Table showing design matrix with randomization and center points

This design would be improved by adding at least 3 centerpoint runs placed at the beginning, middle and end of the experiment. The final design matrix is shown below:

TABLE 3.9  The 2³ Full Factorial Replicated Twice with Random Run Order Indicated and Center Point Runs Added

Random Order	Standard Order	X1	X2	X3
1		0	0	0
2	5	-1	-1	+1
3	15	-1	+1	+1
4	9	-1	-1	-1
5	7	-1	+1	+1
6	3	-1	+1	-1
7	12	+1	+1	-1
8	6	+1	-1	+1
9		0	0	0
10	4	+1	+1	-1
11	2	+1	-1	-1
12	13	-1	-1	+1
13	8	+1	+1	+1
14	16	+1	+1	+1
15	1	-1	-1	-1
16	14	+1	-1	+1
17	11	-1	+1	-1
18	10	+1	-1	-1
19		0	0	0