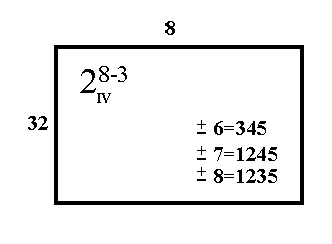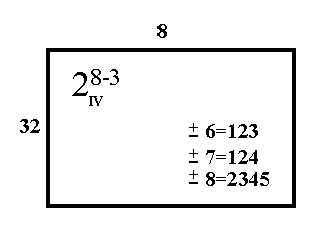5. Process Improvement
5.3. Choosing an experimental design
5.3.3. How do you select an experimental design?
5.3.3.4. Fractional factorial designs

5.3.3.4.4.

Fractional factorial design specifications and design resolution

Generating relation and diagram for the 2^8-3 fractional factorial design

We considered the 2^3-1 design in the previous section and saw that its generator written in "I = ... " form is {I = +123}. Next we look at a one-eighth fraction of a 2⁸ design, namely the 2^8-3 fractional factorial design. Using a diagram similar to Figure 3.5, we have the following:

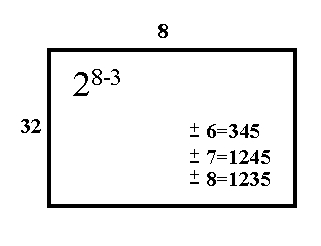
FIGURE 3.6: Specifications for a 2^8-3 Design

2^8-3 design has 32 runs

Figure 3.6 tells us that a 2^8-3 design has 32 runs, not including centerpoint runs, and eight factors. There are three generators since this is a 1/8 = 2^-3 fraction (in general, a 2^k-p fractional factorial needs p generators which define the settings for p additional factor columns to be added to the 2^k-p full factorial design columns - see the following detailed description for the 2^8-3 design).

How to Construct a Fractional Factorial Design From the Specification

Rule for constructing a fractional factorial design

In order to construct the design, we do the following:

1. Write down a full factorial design in standard order for k-p factors (8-3 = 5 factors for the example above). In the specification above we start with a 2⁵ full factorial design. Such a design has 2⁵ = 32 rows.

2. Add a sixth column to the design table for factor 6, using 6 = 345 (or 6 = -345) to manufacture it (i.e., create the new column by multiplying the indicated old columns together).

3. Do likewise for factor 7 and for factor 8, using the appropriate design generators given in Figure 3.6.

4. The resultant design matrix gives the 32 trial runs for an 8-factor fractional factorial design. (When actually running the experiment, we would of course randomize the run order.

Design generators

We note further that the design generators, written in `I = ...' form, for the principal 2^8-3 fractional factorial design are:

{ I = + 3456; I = + 12457; I = +12358 }.

These design generators result from multiplying the "6 = 345" generator by "6" to obtain "I = 3456" and so on for the other two generators.

"Defining relation" for a fractional factorial design

The total collection of design generators for a factorial design, including all new generators that can be formed as products of these generators, is called a defining relation. There are seven "words", or strings of numbers, in the defining relation for the 2^8-3 design, starting with the original three generators and adding all the new "words" that can be formed by multiplying together any two or three of these original three words. These seven turn out to be I = 3456 = 12457 = 12358 = 12367 = 12468 = 3478 = 5678. In general, there will be (2^p -1) words in the defining relation for a 2^k-p fractional factorial.

Definition of "Resolution"

The length of the shortest word in the defining relation is called the resolution of the design. Resolution describes the degree to which estimated main effects are aliased (or confounded) with estimated 2-level interactions, 3-level interactions, etc.

Notation for resolution (Roman numerals)

The length of the shortest word in the defining relation for the 2^8-3 design is four. This is written in Roman numeral script, and subscripted as \( 2_{IV}^{8-3} \). Note that the 2^3-1 design has only one word, "I = 123" (or "I = -123"), in its defining relation since there is only one design generator, and so this fractional factorial design has resolution three; that is, we may write \( 2_{III}^{3-1} \).

Diagram for a 2^8-3 design showing resolution

Now Figure 3.6 may be completed by writing it as:

FIGURE 3.7: Specifications for a 2^8-3, Showing Resolution IV

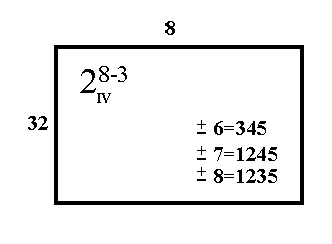
Resolution and confounding

The design resolution tells us how badly the design is confounded. Previously, in the 2^3-1 design, we saw that the main effects were confounded with two-factor interactions. However, main effects were not confounded with other main effects. So, at worst, we have 3=12, or 2=13, etc., but we do not have 1=2, etc. In fact, a resolution II design would be pretty useless for any purpose whatsoever!

Similarly, in a resolution IV design, main effects are confounded with at worst three-factor interactions. We can see, in Figure 3.7, that 6=345. We also see that 36=45, 34=56, etc. (i.e., some two-factor interactions are confounded with certain other two-factor interactions) etc.; but we never see anything like 2=13, or 5=34, (i.e., main effects confounded with two-factor interactions).

The complete first-order interaction confounding for the given 2^8-3 design

The complete confounding pattern, for confounding of up to two-factor interactions, arising from the design given in Figure 3.7 is

34 = 56 = 78
35 = 46
36 = 45
37 = 48
38 = 47
57 = 68
58 = 67

All of these relations can be easily verified by multiplying the indicated two-factor interactions by the generators. For example, to verify that 38= 47, multiply both sides of 8=1235 by 3 to get 38=125. Then, multiply 7=1245 by 4 to get 47=125. From that it follows that 38=47.

One or two factors suspected of possibly having significant first-order interactions can be assigned in such a way as to avoid having them aliased

For this \( 2_{IV}^{8-3} \) fractional factorial design, 15 two-factor interactions are aliased (confounded) in pairs or in a group of three. The remaining 28 - 15 = 13 two-factor interactions are only aliased with higher-order interactions (which are generally assumed to be negligible). This is verified by noting that factors "1" and "2" never appear in a length-4 word in the defining relation. So, all 13 interactions involving "1" and "2" are clear of aliasing with any other two factor interaction.

If one or two factors are suspected of possibly having significant first-order interactions, they can be assigned in such a way as to avoid having them aliased.

Higher resoulution designs have less severe confounding, but require more runs

A resolution IV design is "better" than a resolution III design because we have less-severe confounding pattern in the 'IV' than in the 'III' situation; higher-order interactions are less likely to be significant than low-order interactions.

A higher-resolution design for the same number of factors will, however, require more runs and so it is 'worse' than a lower order design in that sense.

Resolution V designs for 8 factors

Similarly, with a resolution V design, main effects would be confounded with four-factor (and possibly higher-order) interactions, and two-factor interactions would be confounded with certain three-factor interactions. To obtain a resolution V design for 8 factors requires more runs than the 2^8-3 design. One option, if estimating all main effects and two-factor interactions is a requirement, is a \( 2_{V}^{8-3} \) design. However, a 48-run alternative (John's 3/4 fractional factorial) is also available.

There are many choices of fractional factorial designs - some may have the same number of runs and resolution, but different aliasing patterns.

Note: There are other \( 2_{V}^{8-3} \) fractional designs that can be derived starting with different choices of design generators for the "6", "7" and "8" factor columns. However, they are either equivalent (in terms of the number of words of length of length of four) to the fraction with generators 6 = 345, 7 = 1245, 8 = 1235 (obtained by relabeling the factors), or they are inferior to the fraction given because their defining relation contains more words of length four (and therefore more confounded two-factor interactions). For example, the \( 2_{V}^{8-3} \) design with generators 6 = 12345, 7 = 135, and 8 = 245 has five length-four words in the defining relation (the defining relation is I = 123456 = 1357 = 2458 = 2467 = 1368 = 123478 = 5678). As a result, this design would confound more two factor-interactions (23 out of 28 possible two-factor interactions are confounded, leaving only "12", "14", "23", "27" and "34" as estimable two-factor interactions).

Diagram of an alternative way for generating the 2^8-3 design

As an example of an equivalent "best" \( 2_{V}^{8-3} \) fractional factorial design, obtained by "relabeling", consider the design specified in Figure 3.8.

FIGURE 3.8: Another Way of Generating the 2^8-3 Design

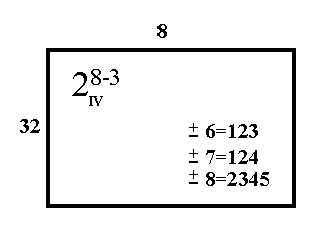
This design is equivalent to the design specified in Figure 3.7 after relabeling the factors as follows: 1 becomes 5, 2 becomes 8, 3 becomes 1, 4 becomes 2, 5 becomes 3, 6 remains 6, 7 becomes 4 and 8 becomes 7.

Minimum aberration

A table given later in this chapter gives a collection of useful fractional factorial designs that, for a given k and p, maximize the possible resolution and minimize the number of short words in the defining relation (which minimizes two-factor aliasing). The term for this is "minimum aberration".

Design Resolution Summary

Commonly used design Resolutions

The meaning of the most prevalent resolution levels is as follows:

Resolution III Designs

Main effects are confounded (aliased) with two-factor interactions.

Resolution IV Designs

No main effects are aliased with two-factor interactions, but two-factor interactions are aliased with each other.

Resolution V Designs

No main effect or two-factor interaction is aliased with any other main effect or two-factor interaction, but two-factor interactions are aliased with three-factor interactions.