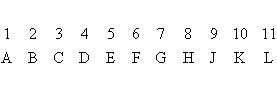5.
Process Improvement
5.3.
Choosing an experimental design
5.3.3.
How do you select an experimental design?
5.3.3.4.
Fractional factorial designs
5.3.3.4.7.
|
Summary tables of useful fractional factorial designs
|
|
|
Useful fractional factorial designs for up to 10 factors are
summarized here
|
There are very useful summaries of two-level fractional factorial
designs for up to 11 factors, originally published in the book
Statistics for Experimenters by G.E.P. Box, W.G. Hunter, and
J.S. Hunter (New York, John Wiley & Sons, 1978) and also given
in the book Design and Analysis of Experiments, 5th edition
by Douglas C. Montgomery (New York, John Wiley & Sons, 2000).
|
|
Generator column notation can use either numbers or letters for the
factor columns
|
They differ in the notation for the
design generators. Box, Hunter,
and Hunter use numbers (as we did in our
earlier discussion) and Montgomery
uses capital letters according to the following scheme:
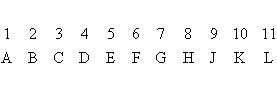Notice the absence of the letter I. This is usually reserved for the
intercept column that is identically 1. As an example of the letter
notation, note that the design generator "6 = 12345" is equivalent to
"F = ABCDE".
|
|
Details of the design generators, the defining relation, the
confounding structure, and the design matrix
|
TABLE 3.17 catalogs these useful fractional factorial designs using
the notation previously described in FIGURE
3.7.
Clicking on the
\( 2_{R}^{k-p} \)
specification for a given design provides details (courtesy of Dataplot
files) of the design generators, the defining relation, the confounding
structure (as far as main effects and two-level interactions are
concerned), and the design matrix. The notation used follows our
previous labeling of factors with numbers, not letters.
|
|
Click on the design specification in the table below and a text file
with details about the design can be viewed or saved
|
TABLE 3.17: Summary of Useful Fractional
Factorial Designs
|
