5. Process Improvement
5.3. Choosing an experimental design
5.3.3. How do you select an experimental design?

5.3.3.6.

Response surface designs

Response surface models may involve just main effects and interactions or they may also have quadratic and possibly cubic terms to account for curvature

Earlier, we described the response surface method (RSM) objective. Under some circumstances, a model involving only main effects and interactions may be appropriate to describe a response surface when

1. Analysis of the results revealed no evidence of "pure quadratic" curvature in the response of interest (i.e., the response at the center approximately equals the average of the responses at the factorial runs).

2. The design matrix originally used included the limits of the factor settings available to run the process.

Equations for quadratic and cubic models

In other circumstances, a complete description of the process behavior might require a quadratic or cubic model:

Quadratic
\( \begin{array}{lcl} \hat{y} & = & \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_ 3 + \beta_{12}x_{1}x_{2} + \beta_{13}x_{1}x_{3} + \\ & & \beta_{23}x_{2}x_{3} + \beta_{11}x_{1}^{2} + \beta_{22}x_{2}^{2} + \beta_{33}x_{3}^{2} \end{array} \)

Cubic
\( \begin{array}{lcl} \hat{y} & = & \mbox{quadratic model} + \beta_{123}x_{1}x_{2}x_{3} + \beta_{112}x_{1}^{2}x_{2} + \beta_{113}x_{1}^{2}x_{3} + \\ & & \beta_{122}x_{1}x_{2}^{2} + \beta_{133}x_{1}x_{3}^{2} + \beta_{223}x_{2}^{2}x_{3} + \beta_{233}x_{2}x_{3}^{2} + \\ & & \beta_{111}x_{1}^{3} + \beta_{222}x_{2}^{3} + \beta_{333}x_{3}^{3} + \end{array} \)

These are the full models, with all possible terms, rarely would all of the terms be needed in an application.

Quadratic models almost always sufficient for industrial applications

If the experimenter has defined factor limits appropriately and/or taken advantage of all the tools available in multiple regression analysis (transformations of responses and factors, for example), then finding an industrial process that requires a third-order model is highly unusual. Therefore, we will only focus on designs that are useful for fitting quadratic models. As we will see, these designs often provide lack of fit detection that will help determine when a higher-order model is needed.

General quadratic surface types

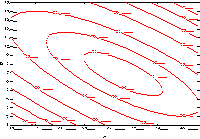
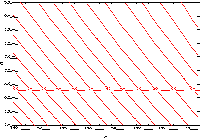
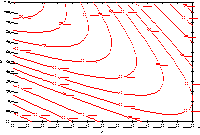
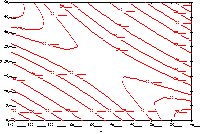
Figures 3.9 to 3.12 identify the general quadratic surface types that an investigator might encounter 
 
 

FIGURE 3.9  A Response Surface "Peak"	FIGURE 3.10   A Response Surface "Hillside"
FIGURE 3.11   A Response Surface "Rising Ridge"	FIGURE 3.12  A Response Surface "Saddle"

Factor Levels for Higher-Order Designs

Possible behaviors of responses as functions of factor settings

Figures 3.13 through 3.15 illustrate possible behaviors of responses as functions of factor settings. In each case, assume the value of the response increases from the bottom of the figure to the top and that the factor settings increase from left to right.

FIGURE 3.13 Linear Function	FIGURE 3.14 Quadratic Function	FIGURE 3.15 Cubic Function

A two-level experiment with center points can detect, but not fit, quadratic effects

If a response behaves as in Figure 3.13, the design matrix to quantify that behavior need only contain factors with two levels -- low and high. This model is a basic assumption of simple two-level factorial and fractional factorial designs. If a response behaves as in Figure 3.14, the minimum number of levels required for a factor to quantify that behavior is three. One might logically assume that adding center points to a two-level design would satisfy that requirement, but the arrangement of the treatments in such a matrix confounds all quadratic effects with each other. While a two-level design with center points cannot estimate individual pure quadratic effects, it can detect them effectively.

Three-level factorial design

A solution to creating a design matrix that permits the estimation of simple curvature as shown in Figure 3.14 would be to use a three-level factorial design. Table 3.21 explores that possibility.

Four-level factorial design

Finally, in more complex cases such as illustrated in Figure 3.15, the design matrix must contain at least four levels of each factor to characterize the behavior of the response adequately.

3-level factorial designs can fit quadratic models but they require many runs when there are more than 4 factors

TABLE 3.21 Three-level Factorial Designs

Number of Factors	Treatment Combinations 3k Factorial	Number of Coefficients Quadratic Empirical Model
2	9	6
3	27	10
4	81	15
5	243	21
6	729	28

Fractional factorial designs created to avoid such a large number of runs

Two-level factorial designs quickly become too large for practical application as the number of factors investigated increases. This problem was the motivation for creating 'fractional factorial' designs. Table 3.21 shows that the number of runs required for a 3^k factorial becomes unacceptable even more quickly than for 2^k designs. The last column in Table 3.21 shows the number of terms present in a quadratic model for each case.

Number of runs large even for modest number of factors

With only a modest number of factors, the number of runs is very large, even an order of magnitude greater than the number of parameters to be estimated when k isn't small. For example, the absolute minimum number of runs required to estimate all the terms present in a four-factor quadratic model is 15: the intercept term, 4 main effects, 6 two-factor interactions, and 4 quadratic terms.

The corresponding 3^k design for k = 4 requires 81 runs.

Complex alias structure and lack of rotatability for 3-level fractional factorial designs

Considering a fractional factorial at three levels is a logical step, given the success of fractional designs when applied to two-level designs. Unfortunately, the alias structure for the three-level fractional factorial designs is considerably more complex and harder to define than in the two-level case.

Additionally, the three-level factorial designs suffer a major flaw in their lack of 'rotatability.'

Rotatability of Designs

"Rotatability" is a desirable property not present in 3-level factorial designs

In a rotatable design, the variance of the predicted values of y is a function of the distance of a point from the center of the design and is not a function of the direction the point lies from the center. Before a study begins, little or no knowledge may exist about the region that contains the optimum response. Therefore, the experimental design matrix should not bias an investigation in any direction.

Contours of variance of predicted values are concentric circles

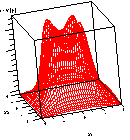
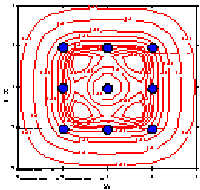
In a rotatable design, the contours associated with the variance of the predicted values are concentric circles. Figures 3.16 and 3.17 (adapted from Box and Draper, `Empirical Model Building and Response Surfaces,' page 485) illustrate a three-dimensional plot and contour plot, respectively, of the `information function' associated with a 3² design.

Information function

The information function is: \( \frac{1}{V(\hat{y})} \)

with V denoting the variance (of the predicted value \( \hat{y} \).

Each figure clearly shows that the information content of the design is not only a function of the distance from the center of the design space, but also a function of direction.

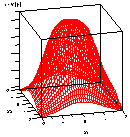
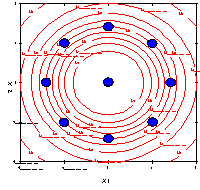
Graphs of the information function for a rotatable quadratic design

Figures 3.18 and 3.19 are the corresponding graphs of the information function for a rotatable quadratic design. In each of these figures, the value of the information function depends only on the distance of a point from the center of the space. 

FIGURE 3.16  Three-Dimensional Illustration for the Information Function of a 32 Design	FIGURE 3.17  Contour Map of the Information Function for a 32 Design
FIGURE 3.18  Three-Dimensional Illustration of the Information Function for a Rotatable Quadratic Design for Two Factors	FIGURE 3.19  Contour Map of the Information Function for a Rotatable Quadratic Design for Two Factors

Classical Quadratic Designs

Central composite and Box-Behnken designs

Introduced during the 1950's, classical quadratic designs fall into two broad categories: Box-Wilson central composite designs and Box-Behnken designs. The next sections describe these design classes and their properties.