5.5. Advanced topics
5.5.3. How do you optimize a process?
5.5.3.2. Multiple response case
5.5.3.2.2. |
Multiple responses: The desirability approach |
For each response Yi(x), a desirability function di(Yi) assigns numbers between 0 and 1 to the possible values of Yi, with di(Yi) = 0 representing a completely undesirable value of Yi and di(Yi) = 1 representing a completely desirable or ideal response value. The individual desirabilities are then combined using the geometric mean, which gives the overall desirability D:
-
\( D = \left( d_{1}(Y_{1}) d_{2}(Y_{2}) \cdots
d_{k}(Y_{k})\right) ^{1/k} \)
-
\(
d_{i}(\hat{Y}_{i}) =
\left\{ \begin{array}{ll}
0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) < L_{i} \\
\left( \frac{\hat{Y}_{i}(x) - L_{i}} {T_{i} - L_{i}}
\right) ^{s} &
\mbox{if } \hspace{.1in}
L_{i} \le \hat{Y}_{i}(x) \le T_{i} \\
\left( \frac{\hat{Y}_{i}(x) - U_{i}} {T_{i} - U_{i}}
\right) ^{t} &
\mbox{if } \hspace{.1in}
T_{i} \le \hat{Y}_{i}(x) \le U_{i} \\
0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) > U_{i}
\end{array}
\right.
\)
-
\(
d_{i}(\hat{Y}_{i}) =
\left\{ \begin{array}{ll}
0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) < L_{i} \\
\left( \frac{\hat{Y}_{i}(x) - L_{i}} {T_{i} - L_{i}}
\right) ^{s} &
\mbox{if } \hspace{.1in}
L_{i} \le \hat{Y}_{i}(x) \le T_{i} \\
1.0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) > T_{i}
\end{array}
\right.
\)
-
\(
d_{i}(\hat{Y}_{i}) =
\left\{ \begin{array}{ll}
1.0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) < T_{i} \\
\left( \frac{\hat{Y}_{i}(x) - U_{i}} {T_{i} - U_{i}}
\right) ^{s} &
\mbox{if } \hspace{.1in}
T_{i} \le \hat{Y}_{i}(x) \le U_{i} \\
0 & \mbox{if } \hspace{.1in} \hat{Y}_{i}(x) > U_{i}
\end{array}
\right.
\)
- Conduct experiments and fit response models for all k responses;
- Define individual desirability functions for each response;
- Maximize the overall desirability D with respect to the controllable factors.
| Source | Desired range |
|---|---|
|
|
|
| PICO Abrasion index, Y1 | 120 < Y1 |
| 200% modulus, Y2 | 1000 < Y2 |
| Elongation at break, Y3 | 400 < Y3 < 600 |
| Hardness, Y4 | 60 < Y4 < 75 |
|
Run Number |
x1 | x2 | x3 | Y1 | Y2 | Y3 | Y4 |
|---|---|---|---|---|---|---|---|
|
|
|||||||
| 1 | -1.00 | -1.00 | -1.00 | 102 | 900 | 470 | 67.5 |
| 2 | +1.00 | -1.00 | -1.00 | 120 | 860 | 410 | 65.0 |
| 3 | -1.00 | +1.00 | -1.00 | 117 | 800 | 570 | 77.5 |
| 4 | +1.00 | +1.00 | -1.00 | 198 | 2294 | 240 | 74.5 |
| 5 | -1.00 | -1.00 | +1.00 | 103 | 490 | 640 | 62.5 |
| 6 | +1.00 | -1.00 | +1.00 | 132 | 1289 | 270 | 67.0 |
| 7 | -1.00 | +1.00 | +1.00 | 132 | 1270 | 410 | 78.0 |
| 8 | +1.00 | +1.00 | +1.00 | 139 | 1090 | 380 | 70.0 |
| 9 | -1.63 | 0.00 | 0.00 | 102 | 770 | 590 | 76.0 |
| 10 | +1.63 | 0.00 | 0.00 | 154 | 1690 | 260 | 70.0 |
| 11 | 0.00 | -1.63 | 0.00 | 96 | 700 | 520 | 63.0 |
| 12 | 0.00 | +1.63 | 0.00 | 163 | 1540 | 380 | 75.0 |
| 13 | 0.00 | 0.00 | -1.63 | 116 | 2184 | 520 | 65.0 |
| 14 | 0.00 | 0.00 | +1.63 | 153 | 1784 | 290 | 71.0 |
| 15 | 0.00 | 0.00 | 0.00 | 133 | 1300 | 380 | 70.0 |
| 16 | 0.00 | 0.00 | 0.00 | 133 | 1300 | 380 | 68.5 |
| 17 | 0.00 | 0.00 | 0.00 | 140 | 1145 | 430 | 68.0 |
| 18 | 0.00 | 0.00 | 0.00 | 142 | 1090 | 430 | 68.0 |
| 19 | 0.00 | 0.00 | 0.00 | 145 | 1260 | 390 | 69.0 |
| 20 | 0.00 | 0.00 | 0.00 | 142 | 1344 | 390 | 70.0 |
(The reader can download the data as a text file.)
-
\( \begin{array}{lcl}
\hat{Y}_{1} & = & 139.12 + 16.49 x_{1} + 17.88 x_{2} + 2.21 x_{3} \\
& & -4.01 x_{1}^{2} - 3.45 x_{2}^{2} -
1.57 x_{3}^{2} \\
& & + 5.12 x_{1} x_{2} - 7.88 x_{1} x_{3} -
7.13 x_{2} x_{3}
\end{array}
\)
-
\( \begin{array}{lcl}
\hat{Y}_{2} & = & 1261.13 + 268.15 x_{1} + 246.5 x_{2} -
102.6 x_{3} \\
& & - 83.57 x_{1}^{2} - 124.92 x_{2}^{2} +
199.2 x_{3}^{2} \\
& & + 69.37 x_{1} x_{2} - 104.38 x_{1} x_{3} -
94.13 x_{2} x_{3}
\end{array}
\)
-
\( \hat{Y}_{3} = 417.5 - 99.67 x_{1} - 31.4 x_{2} - 27.42 x_{3} \)
\( \begin{array}{lcl} \hat{Y}_{4} & = & 68.91 - 1.41 x_{1} + 4.32 x_{2} + 0.21 x_{3} \\ & & + 1.56 x_{1}^{2} + 0.058 x_{2}^{2} - 0.32 x_{3}^{2} \\ & & - 1.62 x_{1} x_{2} + 0.25 x_{1} x_{3} - 0.12 x_{2} x_{3} \end{array} \)
(R2 = 0.8667 and adjusted R2 = 0.7466).
Note that no interactions were significant for response 3 and that the fit for response 2 is quite poor.
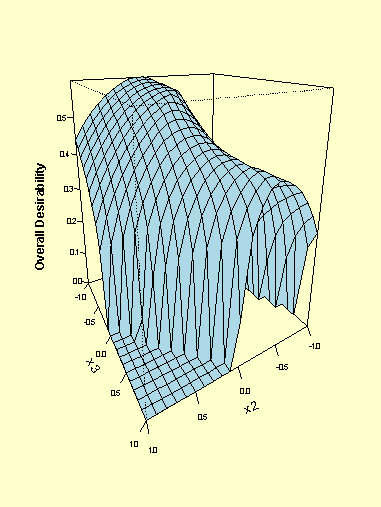
| \( d_{1}(\hat{Y}_{1}) = 0.34 \) | \( (\hat{Y}_{1}(x^{*}) = 136.4) \) |
| \( d_{2}(\hat{Y}_{2}) = 1.0 \) | \( (\hat{Y}_{2}(x^{*}) = 1571.05) \) |
| \( d_{3}(\hat{Y}_{3}) = 0.49 \) | \( (\hat{Y}_{3}(x^{*}) = 450.56) \) |
| \( d_{4}(\hat{Y}_{4}) = 0.76 \) | \( (\hat{Y}_{4}(x^{*}) = 69.26) \) |