5.5. Advanced topics
5.5.9. An EDA approach to experimental design
5.5.9.5. |
Block plot |
- What are the important factors (including interactions)?
- What are the best settings for these important factors?
Due to the ability of the block plot to determine whether a factor is important over all settings of all other factors, the block plot is also referred to as a DOE robustness plot.
- Important factors (of the k factors and the \( \left( \begin{array}{c} k \\ 2 \end{array} \right) \) 2-factor interactions); and
- Best settings of the important factors.
- The first block plot asks the question: "Is factor X1 important?
- The second block plot asks the question: "Is factor X2 important?
- Continue for the remaining factors.
- Vertical Axis: Response
- Horizontal Axis: All 2k-1 possible
combinations of the (k-1) non-target factors (that
is, "robustness" factors). For example, for the block plot
focusing on factor X1 from a 23 full factorial
experiment, the horizontal axis will consist of all
23-1 = 4 distinct combinations of factors X2
and X3. We create this robustness factors axis because
we are interested in determining if X1 is important
robustly. That is, we are interested in whether X1 is
important not only in a general/summary kind of way, but also
whether the importance of X is universally and
consistently valid over each of the 23-1 = 4
combinations of factors X2 and X3. These four
combinations are (X2, X3) = (+, +), (+, -), (-, +),
and (-, -). The robustness factors on the horizontal axis change
from one block plot to the next. For example, for the
k = 3 factor case:
- the block plot targeting X1 will have robustness factors X2 and X3;
- the block plot targeting X2 will have robustness factors X1 and X3;
- the block plot targeting X3 will have robustness factors X1 and X2.
- Plot Character: The setting (- or +) for the target factor Xi. Each point in a block plot has an associated setting for the target factor Xi. If Xi = "-", the corresponding plot point will be "-"; if Xi = "+", the corresponding plot point will be "+".
- one plot point for Xi = "-"; and
- the other plot point for Xi = "+".
Large within-block differences (that is, tall blocks) indicate a large local effect on the response which, since all robustness factors are fixed for a given block, can only be attributed to the target factor. This identifies an "important" target factor. Small within-block differences (small blocks) indicate that the target factor Xi is unimportant.
For a given block plot, the specific question of interest is thus
-
Is the target factor Xi important? That is,
as we move within a block from the target factor setting of "-" to
the target factor setting of "+", does the response variable
value change by a large amount?
In summary, important factors will have both
- consistently large block heights; and
- consistent +/- sign arrangements
- Important factors (including 2-factor interactions);
- Best settings for these factors.
Important factors (including 2-factor interactions):
Look at each of the k block plots. Within a given block plot,
-
Are the corresponding block heights
consistently large as we scan across the
within-plot robustness factor
settings--yes/no; and are the within-block
sign patterns (+ above -, or - above +)
consistent across all robustness factors
settings--yes/no?
- Which plot has the consistently largest block heights,
along with consistent arrangement of within-block +'s
and -'s? This defines the "most important factor".
- Which plot has the consistently next-largest block heights,
along with consistent arrangement of within-block
+'s and -'s? This defines the "second most important
factor".
- Continue for the remaining factors.
Important Special Case; Large but Inconsistent:
What happens if the block heights are large but not consistent? Suppose, for example, a 23 factorial experiment is being analyzed and the block plot focusing on factor X1 is being examined and interpreted so as to address the usual question of whether factor X1 is important.
Let us consider in some detail how such a block plot might appear. This X1 block plot will have 23-1 = 4 combinations of the robustness factors X2 and X3 along the horizontal axis in the following order:
-
(X2, X3) = (+, +); (X2, X3) = (+, -);
(X2, X3) = (-, +); (X2, X3) = (-, -).
| (X2, X3) | block height (= local X1 effect) |
| (+, +) | 30 |
| (+, -) | 29 |
| (-, +) | 29 |
| (-, -) | 31 |
then from binomial considerations there is one chance in 24-1 = 1/8 \( \approx \) 12.5 % of the the four local X1 effects having the same sign (i.e., all positive or all negative). The usual statistical cutoff of 5 % has not been achieved here, but the 12.5 % is suggestive. Further, the consistency of the four X1 effects (all near 30) is evidence of a robustness of the X effect over the settings of the other two factors. In summary, the above suggests:
- Factor 1 is probably important (the issue of how large the effect has to be in order to be considered important will be discussed in more detail in a later section); and
- The estimated factor 1 effect is about 30 units.
| (X2, X3) | block height (= local X1 effect) |
| (+, +) | 30 |
| (+, -) | 20 |
| (-, +) | 30 |
| (-, -) | 20 |
then how is this to be interpreted?
The key here to such interpretation is that the block plot is telling us that the estimated X1 effect is in fact at least 20 units, but not consistent. The effect is changing, but it is changing in a structured way. The "trick" is to scan the X2 and X3 settings and deduce what that substructure is. Doing so from the above table, we see that the estimated X1 effect is 30
- for point 1 (X2, X3) = (+, +) and
- for point 3 (X2, X3) = (-, +)
- for point 2 (X2, X3) = (+, -) and
- for point 4 (X2, X3) = (-, -)
- 30 whenever X3 = "+"
- 20 whenever X3 = "-"
- factor X1 is probably important;
- the estimated factor X1 effect is 25 (the average of 30, 20, 30, and 20);
- the X1*X3 interaction is probably important;
- the estimated X1*X3 interaction is about 10 (the change in the factor X1 effect as X3 changes = 30 - 20 = 10);
- hence the X1*X3 interaction is less important than the X1 effect.
The block plot gives us the structure and the detail to allow such conclusions to be drawn and to be understood. It is a valuable adjunct to the previous analysis steps.
Best settings:
After identifying important factors, it is also of use to determine the best settings for these factors. As usual, best settings are determined for main effects only (since main effects are all that the engineer can control). Best settings for interactions are not done because the engineer has no direct way of controlling them.
In the block plot context, this determination of best factor settings is done simply by noting which factor setting (+ or -) within each block is closest to that which the engineer is ultimately trying to achieve. In the defective springs case, since the response variable is percent acceptable springs, we are clearly trying to maximize (as opposed to minimize, or hit a target) the response and the ideal optimum point is 100 %. Given this, we would look at the block plot of a given important factor and note within each block which factor setting (+ or -) yields a data value closest to 100 % and then select that setting as the best for that factor.
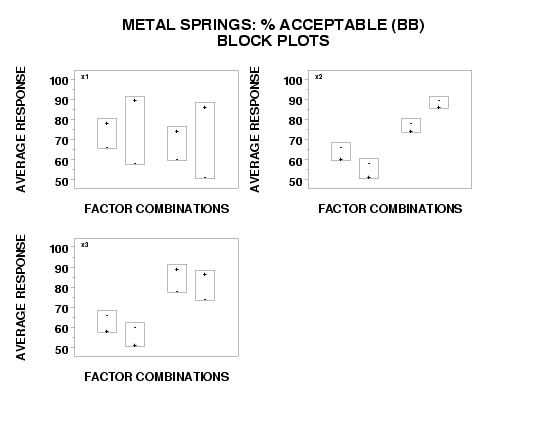
From the defective springs block plots, we would thus conclude that
- the best setting for factor 1 is +;
- the best setting for factor 2 is -;
- the best setting for factor 3 cannot be easily determined.
- Unranked list of important factors (including interactions):
- X1 is important;
- X2 is important;
- X1*X3 is important.
- Best Settings:
-
(X1, X2, X3) = (+, -, ?) = (+1, -1, ?)