5.5.9.8. Half-normal probability plot

5. Process Improvement
5.5. Advanced topics
5.5.9. An EDA approach to experimental design

5.5.9.8. Half-normal probability plot

Purpose

The half-normal probability plot answers the question:

What are the important factors (including interactions)? Quantitatively, the estimated effect of a given main effect or interaction and its rank relative to other main effects and interactions is given via least squares estimation (that is, forming effect estimates that minimize the sum of the squared differences between raw data and the fitted values from such estimates). Having such estimates in hand, one could then construct a list of the main effects and interactions ordered by the effect magnitude.

The half-normal probability plot is a graphical tool that uses these ordered estimated effects to help assess which factors are important and which are unimportant.

A half-normal distribution is the distribution of the |X| with X having a normal distribution.

Output

The outputs from the half-normal probablity plot are

Primary: Grouping of factors and interactions into two categories: important and unimportant. For full factorial designs, interactions include the full complement of interactions of all orders; for fractional factorial designs, interactions include only some, and occasionally none, of the actual interactions (when they aren't estimable).
Secondary: Ranked list of factors and interactions from most important down to least important.

Definition

A half-normal probability plot is formed by

Vertical Axis: Ordered (largest to smallest) absolute value of the estimated effects for the main factors and available interactions. If n data points (no replication) have been collected, then typically (n-1) effects will be estimated and the (n-1) |effects| will be plotted.
Horizontal Axis: (n-1) theoretical order statistic medians from a half-normal distribution. These (n-1) values are not data-dependent. They depend only on the half-normal distribution and the number of items plotted (= n-1). The theoretical medians represent an "ideal" typical ordered data set that would have been obtained from a random drawing of (n-1) samples from a half-normal distribution.
Far right margin : Factor/interaction identification:
If the design is a fractional factorial, the confounding structure is provided for main effects and 2-factor interactions.

Motivation

To provide a rationale for the half-normal probability plot, we first dicuss the motivation for the normal probability plot (which also finds frequent use in these 2-level designs).

The basis for the normal probability plot is the mathematical form for each (and all) of the estimated effects. As discussed for the |effects| plot, the estimated effects are the optimal least squares estimates. Because of the orthogonality of the 2^k full factorial and the 2^k-p fractional factorial designs, all least squares estimators for main effects and interactions simplify to the form:

estimated effect = \( \bar{Y} \)(+) - \( \bar{Y} \)(-) with \( \bar{Y} \)(+) the average of all response values for which the factor or interaction takes on a "+" value, and where \( \bar{Y} \)(-) is the average of all response values for which the factor or interaction takes on a "-" value.

Under rather general conditions, the Central Limit Thereom allows that the difference-of-sums form for the estimated effects tends to follow a normal distribution (for a large enough sample size n) a normal distribution.

The question arises as to what normal distribution; that is, a normal distribution with what mean and what standard deviation? Since all estimators have an identical form (a difference of averages), the standard deviations, though unknown, will in fact be the same under the assumption of constant σ. This is good in that it simplifies the normality analysis.

As for the means, however, there will be differences from one effect to the next, and these differences depend on whether a factor is unimportant or important. Unimportant factors are those that have near-zero effects and important factors are those whose effects are considerably removed from zero. Thus, unimportant effects tend to have a normal distribution centered near zero while important effects tend to have a normal distribution centered at their respective true large (but unknown) effect values.

In the simplest experimental case, if the experiment were such that no factors were important (that is, all effects were near zero), the (n-1) estimated effects would behave like random drawings from a normal distribution centered at zero. We can test for such normality (and hence test for a null-effect experiment) by using the normal probability plot. Normal probability plots are easy to interpret. In simplest terms:

if linear, then normal If the normal probability plot of the (n-1) estimated effects is linear, this implies that all of the true (unknown) effects are zero or near-zero. That is, no factor is important.

On the other hand, if the truth behind the experiment is that there is exactly one factor that was important (that is, significantly non-zero), and all remaining factors are unimportant (that is, near-zero), then the normal probability plot of all (n-1) effects is near-linear for the (n-2) unimportant factors and the remaining single important factor would stand well off the line.

Similarly, if the experiment were such that some subset of factors were important and all remaining factors were unimportant, then the normal probability plot of all (n-1) effects would be near-linear for all unimportant factors with the remaining important factors all well off the line.

In real life, with the number of important factors unknown, this suggests that one could form a normal probability plot of the (n-1) estimated effects and draw a line through those (unimportant) effects in the vicinity of zero. This identifies and extracts all remaining effects off the line and declares them as important.

The above rationale and methodology works well in practice, with the net effect that the normal probability plot of the effects is an important, commonly used and successfully employed tool for identifying important factors in 2-level full and factorial experiments. Following the lead of Cuthbert Daniel (1976), we augment the methodology and arrive at a further improvement. Specifically, the sign of each estimate is completely arbitrary and will reverse depending on how the initial assignments were made (e.g., we could assign "-" to treatment A and "+" to treatment B or just as easily assign "+" to treatment A and "-" to treatment B).

This arbitrariness is addressed by dealing with the effect magnitudes rather than the signed effects. If the signed effects follow a normal distribution, the absolute values of the effects follow a half-normal distribution.

In this new context, one tests for important versus unimportant factors by generating a half-normal probability plot of the absolute value of the effects. As before, linearity implies half-normality, which in turn implies all factors are unimportant. More typically, however, the half-normal probability plot will be only partially linear. Unimportant (that is, near-zero) effects manifest themselves as being near zero and on a line while important (that is, large) effects manifest themselves by being off the line and well-displaced from zero.

Plot for defective springs data

The half-normal probability plot of the effects for the defectice springs data set is as follows.

How to interpret

From the half-normal probability plot, we look for the following:

Identifying Important Factors:
Determining the subset of important factors is the most important task of the half-normal probability plot of |effects|. As discussed above, the estimated |effect| of an unimportant factor will typically be on or close to a near-zero line, while the estimated |effect| of an important factor will typically be displaced well off the line.
The separation of factors into important/unimportant categories is thus done by answering the question:
This line of unimportant factors typically encompasses the majority of the points on the plot. The procedure consists, therefore, of the following:
1. identifying this line of near-zero (unimportant) factors; then
2. declaring the remaining off-line factors as important.
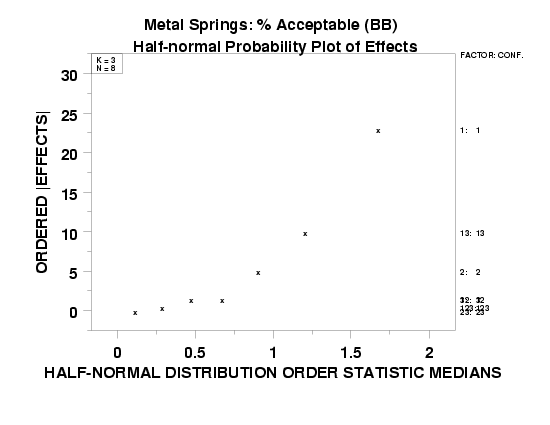
Note that the half-normal probability plot of |effects| and the |effects| plot have the same vertical axis; namely, the ordered |effects|, so the following discussion about right-margin factor identifiers is relevant to both plots. As a consequence of the natural on-line/off-line segregation of the |effects| in half-normal probability plots, factors off-line tend to have far-right labels that are distinct and isolated while factors near the line tend to have far-right labels that are overstruck and hard to read. The rough rule-of-thumb would then be to declare as important those factors/interactions whose far-right labels are easy to distinguish and to declare as unimportant those factors/interactions whose far-right labels are overwritten and hard to distinguish.
Ranked List of Factors (including interactions):
This is a minor objective of the half-normal probability plot (it is better done via the |effects| plot). To determine the ranked list of factors from a half-normal probability plot, simply scan the vertical axis |effects|
1. Which |effect| is largest? Note the factor identifier associated with this largest |effect| (this is the "most important factor").
2. Which |effect| is next in size? Note the factor identifier associated with this next largest |effect| (this is the "second most important factor").
3. Continue for the remaining factors. In practice, the bottom end of the ranked list (the unimportant factors) will be hard to extract because of overstriking, but the top end of the ranked list (the important factors) will be easy to determine.

In summary, it should be noted that since the signs of the estimated effects are arbitrary, we recommend the use of the half-normal probability plot of |effects| technique over the normal probability plot of the |effects|. These probability plots are among the most commonly-employed EDA procedure for identification of important factors in 2-level full and factorial designs. The half-normal probability plot enjoys widespread usage across both "classical" and Taguchi camps. It deservedly plays an important role in our recommended 10-step graphical procedure for the analysis of 2-level designed experiments.

Conclusions for the defective springs data

The application of the half-normal probability plot to the defective springs data set results in the following conclusions:

Ranked list of factors (including interactions):
1. X₁ (most important)
2. X₁*X₃ (next most important)
3. X₂
4. other factors are of lesser importance
Separation of factors into important/unimportant categories: