5. Process Improvement
5.5. Advanced topics
5.5.9. An EDA approach to experimental design

5.5.9.9.

Cumulative residual standard deviation plot

Purpose

The cumulative residual sd (standard deviation) plot answers the question:

What is a good model for the data?

The prior 8 steps in this analysis sequence addressed the two important goals:

1. Factors: determining the most important factors that affect the response, and
2. Settings: determining the best settings for these factors.

In addition to the above, a third goal is of interest:

3. Model: determining a model (that is, a prediction equation) that functionally relates the observed response Y with the various main effects and interactions.

Such a function makes particular sense when all of the individual factors are continuous and ordinal (such as temperature, pressure, humidity, concentration, etc.) as opposed to any of the factors being discrete and non-ordinal (such as plant, operator, catalyst, supplier).

In the continuous-factor case, the analyst could use such a function for the following purposes.

1. Reproduction/Smoothing: predict the response at the observed design points.
2. Interpolation: predict what the response would be at (unobserved) regions between the design points.
3. Extrapolation: predict what the response would be at (unobserved) regions beyond the design points.

For the discrete-factor case, the methods developed below to arrive at such a function still apply, and so the resulting model may be used for reproduction. However, the interpolation and extrapolation aspects do not apply.

In modeling, we seek a function f in the k factors X₁, X₂, ..., X_k such that the predicted values

\( \hat{Y} = f(X_{1}, X_{2}, \ldots , X_{k}) \)

are "close" to the observed raw data values Y. To this end, two tasks exist:

1. Determine a good functional form f;
2. Determine good estimates for the coefficients in that function f.

For example, if we had two factors X₁ and X₂, our goal would be to

1. determine some function f(X₁,X₂); and
2. estimate the parameters in f

such that the resulting model would yield predicted values \( \hat{Y} \) that are as close as possible to the observed response values Y. If the form f has been wisely chosen, a good model will result and that model will have the characteristic that the differences ("residuals" = Y - \( \hat{Y} \)) will be uniformly near zero. On the other hand, a poor model (from a poor choice of the form f) will have the characteristic that some or all of the residuals will be "large".

For a given model, a statistic that summarizes the quality of the fit via the typical size of the n residuals is the residual standard deviation:

\( s_{res} = \sqrt{\frac{\sum_{i=1}^{n}{r_{i}^{2}}}{n-p}} \)

with p denoting the number of terms in the model (including the constant term) and r denoting the ith residual. We are also assuming that the mean of the residuals is zero, which will be the case for models with a constant term that are fit using least squares.

If we have a good-fitting model, s_res will be small. If we have a poor-fitting model, s_res will be large.

For a given data set, each proposed model has its own quality of fit, and hence its own residual standard deviation. Clearly, the residual standard deviation is more of a model-descriptor than a data-descriptor. Whereas "nature" creates the data, the analyst creates the models. Theoretically, for the same data set, it is possible for the analyst to propose an indefinitely large number of models.

In practice, however, an analyst usually forwards only a small, finite number of plausible models for consideration. Each model will have its own residual standard deviation. The cumulative residual standard deviation plot is simply a graphical representation of this collection of residual standard deviations for various models. The plot is beneficial in that

1. good models are distinguished from bad models;
2. simple good models are distinguished from complicated good models.

In summary, then, the cumulative residual standard deviation plot is a graphical tool to help assess

1. which models are poor (least desirable); and
2. which models are good but complex (more desirable); and
3. which models are good and simple (most desirable).

Output

The outputs from the cumulative residual standard deviation plot are

1. Primary: A good-fitting prediction equation consisting of an additive constant plus the most important main effects and interactions.

2. Secondary: The residual standard deviation for this good-fitting model.

Definition

A cumulative residual sd plot is formed by

1. Vertical Axis: Ordered (largest to smallest) residual standard deviations of a sequence of progressively more complicated fitted models.

2. Horizontal Axis: Factor/interaction identification of the last term included into the linear model:
   1 indicates factor X₁;
   2 indicates factor X₂;
   ...
   12 indicates the 2-factor X₁*X₂ interaction
   123 indicates the 3-factor X₁*X₂*X₃ interaction
   etc.

3. Far right margin: Factor/interaction identification (built-in redundancy):
   1 indicates factor X₁;
   2 indicates factor X₂;
   ...
   12 indicates the 2-factor X₁*X₂ interaction
   123 indicates the 3-factor X₁*X₂*X₃ interaction
   etc.

   If the design is a fractional factorial, the confounding structure is provided for main effects and 2-factor interactions.

The cumulative residual standard deviations plot is thus a Pareto-style, largest to smallest, graphical summary of residual standard deviations for a selected series of progressively more complicated linear models.

The plot shows, from left to right, a model with only a constant and the model then augmented by including, one at a time, remaining factors and interactions. Each factor and interaction is incorporated into the model in an additive (rather than in a multiplicative or logarithmic or power, etc. fashion). At any stage, the ordering of the next term to be added to the model is such that it will result in the maximal decrease in the resulting residual standard deviation.

Motivation

This section addresses the following questions:

1. What is a model?
2. How do we select a goodness-of-fit metric for a model?
3. How do we construct a good model?
4. How do we know when to stop adding terms?
5. What is the final form for the model?
6. What are the advantages of the linear model?
7. How do we use the model to generate predicted values?
8. How do we use the model beyond the data domain?
9. What is the best confirmation point for interpolation?
10. How do we use the model for interpolation?
11. How do we use the model for extrapolation?

Plot for defective springs data

Applying the cumulative residual standard deviation plot to the defective springs data set yields the following plot.

How to interpret

As discussed in detail under question 4 in the Motivation section, the cumulative residual standard deviation "curve" will characteristically decrease left to right as we add more terms to the model. The incremental improvement (decrease) tends to be large at the beginning when important factors are being added, but then the decrease tends to be marginal at the end as unimportant factors are being added.

Including all terms would yield a perfect fit (residual standard deviation = 0) but would also result in an unwieldy model. Including only the first term (the average) would yield a simple model (only one term!) but typically will fit poorly. Although a formal quantitative stopping rule can be developed based on statistical theory, a less-rigorous (but good) alternative stopping rule that is graphical, easy to use, and highly effective in practice is as follows:

Keep adding terms to the model until the curve's "elbow" is encountered. The "elbow point" is that value in which there is a consistent, noticeably shallower slope (decrease) in the curve. Include all terms up to (and including) the elbow point (after all, each of these included terms decreased the residual standard deviation by a large amount). Exclude any terms after the elbow point since all such successive terms decreased the residual standard deviation so slowly that the terms were "not worth the complication of keeping".

From the residual standard deviation plot for the defective springs data, we note the following:

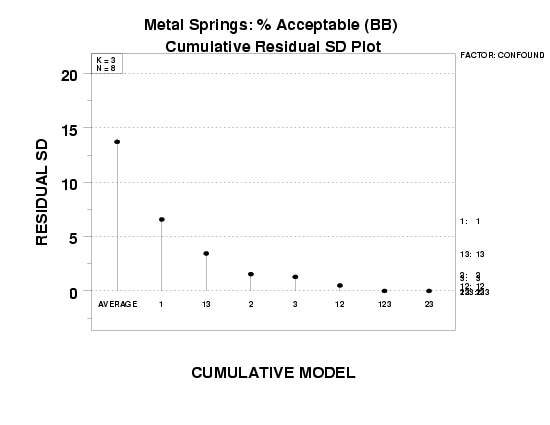
1. The residual standard deviation (rsd) for the "baseline" model
   \( \hat{Y} = \bar{Y} = 71.25 \)

   is s_res = 13.7.

2. As we add the next term, X₁, the rsd drops nearly 7 units (from 13.7 to 6.6).

3. If we add the term X₁*X₃, the rsd drops another 3 units (from 6.6 to 3.4).

4. If we add the term X₂, the rsd drops another 2 units (from 3.4 to 1.5).

5. When the term X₃ is added, the reduction in the rsd (from about 1.5 to 1.3) is negligible.

6. Thereafter to the end, the total reduction in the rsd is from only 1.3 to 0.

In step 5, note that when we have effects of equal magnitude (the X₃ effect is equal to the X₁*X₂ interaction effect), we prefer including a main effect before an interaction effect and a lower-order interaction effect before a higher-order interaction effect.

In this case, the "kink" in the residual standard deviation curve is at the X₂ term. Prior to that, all added terms (including X₂) reduced the rsd by a large amount (7, then 3, then 2). After the addition of X₂, the reduction in the rsd was small (all less than 1): 0.2, then 0.8, then 0.5, then 0.

The final recommended model in this case thus involves p = 4 terms:

1. the average
2. factor X₁
3. the X₁*X₃ interaction
4. factor X₂

The fitted model thus takes on the form

\( \hat{Y} = \bar{Y} + B_{1}X_{1} + B_{13}X_{1}X_{3} + B_{2}X_{2} \)

The least-squares estimates for the coefficients in this model are

\( \hat{Y} \) = 71.25
B₁ = 11.5
B₁₃ = 5
B₂ = -2.5

The B₁ = 11.5, B₁₃ = 5, and B₂ = -2.5 least-squares values are, of course, one half of the estimated effects E₁ = 23, E₁₃ = 10, and E₂ = -5. Effects, calculated as \( \hat{Y} \)(+1) - \( \hat{Y} \)(-1), were previously derived in step 7 of the recommended 10-step DOE analysis procedure.

The final fitted model is thus

\( \hat{Y} = 71.25 + 11.5 X_{1} + 5 X_{1}X_{3} - 2.5 X_{2} \)

Applying this prediction equation to the 8 design points yields: predicted values \( \hat{Y} \) that are close to the data Y, and residuals (Res = Y - \( \hat{Y} \)) that are close to zero:

X1	X2	X3	Y	\( \hat{Y} \)	Res
-	-	-	67	67.25	-0.25
+	-	-	79	80.25	-1.25
-	+	-	61	62.25	-1.25
+	+	-	75	75.25	-0.25
-	-	+	59	57.25	+1.75
+	-	+	90	90.25	-0.25
-	+	+	52	52.25	-0.25
+	+	+	87	85.25	+1.75

Computing the residual standard deviation:

\( s_{res} = \sqrt{ \frac{\sum_{i=1}^{n}{r_{i}^{2}}} {n-p} } \)

with n = 8 data points, and p = 4 estimated coefficients (including the average) yields

s_res = 1.54 (or 1.5 if rounded to 1 decimal place)

The detailed s_res = 1.54 calculation brings us full circle, for 1.54 is the value given above the X₃ term on the cumulative residual standard deviation plot.

Conclusions for the defective springs data

The application of the Cumulative Residual Standard Deviation Plot to the defective springs data set results in the following conclusions:

1. Good-fitting Parsimonious (constant + 3 terms) Model:
   \( \hat{Y} = 71.25 + 11.5 X_{1} + 5 X_{1}X_{3} - 2.5 X_{2} \)

2. Residual Standard Deviation for this Model (as a measure of the goodness-of-fit for the model):
   s_res = 1.54