Familiarity with the basic concepts and techniques from probability theory and mathematical statistics can best be gained by studying suitable textbooks and exercising those concepts and techniques by solving instructive problems. The books by DeGroot and Schervish [2011], Hoel et al. [1971a], Hoel et al. [1971b], Feller [1968], Lindley [1965a], and Lindley [1965b] are highly recommended for this purpose and appropriate for readers who will have studied mathematical calculus in university courses for science and engineering majors.
This document aims to provide an overview of some of these concepts and techniques that have proven useful in applications to the characterization, propagation, and interpretation of measurement uncertainty as described, for example, by Morgan and Henrion [1992] and Taylor and Kuyatt [1994], and in guidance documents produced by international organizations, including the Guide to the expression of uncertainty in measurement (GUM) [Joint Committee for Guides in Metrology, 2008a] and its supplements [Joint Committee for Guides in Metrology, 2008b]. However, the examples do not all necessarily show a direct connection to measurement science.
Our basic premises are that probability is best suited to express uncertainty quantitatively, and that Bayesian statistical methods afford the best means to exploit information about quantities of interest that originates from multiple sources, including empirical data gathered for the purpose, and preexisting expert knowledge.
Although there is nothing particularly controversial about the calculus of probability or about the mathematical methods of statistics, both the meaning of probability and the interpretation of the products of statistical inference continue to be subjects of debate.
This debate is meta-probabilistic and meta-statistical, in the same sense as metaphysics employs methods different from the methods of physics to study the world. In fact, the debate is liveliest and most scholarly among professional philosophers [Fitelson, 2007]. However, probabilists and statisticians often participate in it when they take off their professional hats and become philosophers [Neyman, 1977], as any inquisitive person is wont to do, at one time or another.
For this reason, we begin with an overview of some of the meanings that have been assigned to probability (§2) before turning to the calculus of probability (§3). In applications, the devices of this calculus are typically brought into play when considering random variables and probability distributions (§4), in particular to characterize the probability distribution of functions of random variables (§5). Statistical inference (§6) uses all of these devices to produce probabilistic statements about unknown quantity values.
In Truth and Probability [Ramsey, 1926, 1931], Frank Ramsey takes the view that probability is “a branch of logic, the logic of partial belief and inconclusive argument”. In this vein, and more generally, probabilities serve to quantify uncertainty. For example, when one states that, with confidence, the distance between two geodesic marks is within 0.07 m of 936.84 m, one believes that the actual distance most likely lies between 936.77 m and 936.91 m, but still entertains the possibility that it may lie elsewhere. Similarly, a weather service announcement of chance of rain tomorrow for a particular region summarizes an assessment of uncertainty about what will come to pass.
Although relevant to the interpretation of measurement uncertainty, and generally to all applications of probability and statistics, the meaning of probability really is a philosophical issue [Gillies, 2000, Hájek, 2007, Mellor, 2005]. And while there is much disagreement about what probabilities mean, and how they are created to begin with (interpretation and elicitation of probability), there also is essentially universal agreement about how numerical assessments of probability should be manipulated and combined (calculus of probability).
Chances arise in connection with games of chance, and with phenomena that conceivably can recur under essentially the same circumstances. Thus one speaks of the chances of a pair of Kings in a poker hand, or of the chances that the nucleus of an atom of a particular uranium isotope will emit an alpha particle within a given time interval, or of the chances that a person born in France will have blood of type AB. Chances seem to be intrinsic properties of objects or processes in specific environments, maybe propensities for something to happen: their most renowned theorists have been Hans Reichenbach [Reichenbach, 1949], Richard von Mises [von Mises, 1981], and Karl Popper [Popper, 1959].
Credences measure subjective beliefs. They are best illustrated in relation with betting on the outcomes of events one is uncertain about. For example, in this most memorable of bets offered when the thoroughbred Eclipse was about to run against Gower, Tryal, Plume, and Chance in the second heat of the races on May 3rd, 1769, at Epsom Downs: “Eclipse first, the rest nowhere”, with odds of 6-to-4 [Clee, 2007].
The strength or degree of these beliefs can be assessed numerically by techniques that include the observation of betting behavior (actual or virtual), and this assessment can be gauged, and improved, by application of scoring rules [Lindley, 1985].
Dennis Lindley [Lindley, 1985] suggests that degrees of belief can be measured by comparison with a standard, similarly to how length or mass are measured. In general, subjective probabilities can be revealed by judicious application of elicitation methods [Garthwaite et al., 2005].
Consider an urn that contains 100 balls that are identical but for their colors: are black and are white. The urn’s contents are thoroughly mixed, and the standard is the probability of the event of drawing a black ball. Now, given an event , for example that, somewhere in London, it will rain tomorrow, whose probability he wishes to gauge, Peter will select a value for such that he regards gambling on as equivalent to gambling on (for the same prize): in these circumstances, is Peter’s credence on .
The beliefs that credences measure are subjective and personal, hence the probabilities that gauge them purport to a relationship between a particular knowing subject and the object of this subject’s interest. These beliefs certainly are informed by such knowledge as one may have about a situation, but they also are tempered by one’s preferences or tastes, and do not require that a link be drawn explicitly between that knowledge or sentiment and the corresponding bet. Bruno de Finetti [de Finetti, 1937, 1990], Jimmie Savage [Savage, 1972], and Dennis Lindley [Lindley, 2006] have been leading developers of the subjective, personalistic viewpoint.
Logical (or epistemic, that is, involving or relating to knowledge) probabilities measure the degree to which the truth of a proposition justifies, warrants, or rationally supports the truth of another [Carnap, 1962]. For example, when a medical doctor concludes that a positive result in a tuberculin sensitivity test indicates tuberculosis with probability (§3.6), or when measurements made during a total eclipse of the sun overwhelmingly favor Einstein’s theory of gravitation over Newton’s [Dyson et al., 1920].
The fact that scientists or judges may not necessarily or explicitly use probabilities to convey their confidence in theories or in arguments [Glymour, 1980] does not reduce the value that probabilities have in models for the rational process of learning from experience, either for human subjects or for reasoning machines that are programmed to make decisions in situations of uncertainty. In this fashion, probability is an extension of deductive logic, and measures degree of confirmation: it does this objectively because it does not involve subjective personal opinion, hence is as incontrovertible as deduction by any of the forms of classical logic.
The difficulty lies in specifying a starting point, a state of a priori ignorance that is similarly objective and hence universally acceptable. Harold Jeffreys [Jeffreys, 1961] provided maybe the first modern, thorough account of how this may be done. He argued, and illustrated in many substantive examples, that it is fit to address the widest range of scientific problems where one wishes to exploit the information in observational data.
The interpretation of probability as an extension of logic makes it particularly well-suited to applications in measurement science, where it is desirable to be able to treat different uncertainty components, which may have been evaluated using different methods, simultaneously, using a uniform vocabulary, and a single set of technical tools. This concept underlies the treatment of measurement uncertainty in the GUM and in its supplements. Richard Cox [Cox, 1946, 1961] and Edwin Jaynes [Jaynes, 1958, 2003] have articulated cogent arguments in support of this view, and José Bernardo [Bernardo, 1979] and James Berger [Berger, 2006] have greatly expanded it.
Even in situations where, on first inspection, chances seem applicable, closer inspection reveals that something else really is needed.
There may be no obvious reason to doubt that the chance is ½ that a coin tossed to assign sides before a football game will land Heads up. However, if the coin instead is spun on its edge on a table, that chance will be closer to either or than to ½ [Diaconis and Ylvisaker, 1985].
And when it is the magician Persi Warren [DeGroot, 1986] who tosses the coin, then all bets are off because he can manage to toss it so that it always lands Heads up on his hand after he flips it in the air: while the unwary may be willing to bet at even odds on the outcome, for Persi the probability is 1.
And there are situations that naturally lend themselves to, or that even seem to require, multiple interpretations. Take the 20 % chance of rain: does this mean that, of all days when the weather conditions have been similar to today’s in the region the forecast purports to, it has rained some time during the following day with historical frequency of 20 %? Or is this the result of a probabilistic forecast that is to be interpreted epistemically? Maybe it means something else altogether, like: of all things that will fall from the sky tomorrow, 1 in 5 will be a raindrop.
The use of probability as an extension of logic ensures that different people who have the same information (empirical or other) about a measurand should produce the same inferences about it. Example §2.7 illustrates the fact that contextual information relating to a proposition, situation, or event, will influence probabilistic assessments to the extent that different people with different information may, while all acting rationally, produce different uncertainty assessments, and hence different probabilities, for the same proposition, situation, or event.
When probabilities express subjective beliefs, or when they express states of incomplete or imperfect knowledge, different people typically will assign different probabilities to the same statements or events. If they have to reach a consensus on a course of action that is informed by their plural, varied assessments, then they have to engage in a harmonization exercise that preserves the internal coherence of their individual positions. Both statisticians [Stone, 1961, Morris, 1977, Lindley, 1983, Clemen and Winkler, 1999] and philosophers [Bovens and Rabinowicz, 2006, Hartmann and Sprenger, 2011] have addressed this topic.
James and Claire, who both make investments in mining prospects, have been told that samples from a region surveyed recently have mass fractions of titanium averaging 3 g kg-1, give or take 1 g kg-1 (where “give or take” means that the true mass fraction of titanium in the region sampled is between 2 g kg-1 and 4 g kg-1 with 95 % probability). James, however, has also been told that the samples are of a sandstone with grains of ilmenite. On this basis, James may assign a much higher probability than Claire to the proposition that asserts that the region sampled includes an economically viable deposit of titanium ore.
Once numeric probabilities are in hand, irrespective of how they may be interpreted, the same set of rules, or axioms, is used to combine them. We formulate these axioms in the context where probability is regarded as measuring degree of (rational) belief in the truth of propositions, given a particular body of knowledge and universe of discourse, , that makes all the participating elements meaningful.
Let and denote propositions whose probabilities and express degrees of belief about their truth given (or, conditionally upon) the context defined by . The notation denotes the conditional probability of , assuming that is true and given the context defined by . Note that is not necessarily 0 when : for example, the probability is 0 that a point chosen uniformly at random over the surface of the earth will be on the equator; yet the probability is ½ that, conditionally on its being on the equator, its longitude is between 0° and 180° West of the prime meridian at Greenwich, UK.
The axioms for the calculus of probability are these:
Since the roles of and are interchangeable, the multiplication axiom obviously can also be written as .
Most accounts of mathematical probability theory use an additional rule (countable additivity) that ensures that the probability that at least one proposition is true, among countably infinitely many mutually exclusive propositions, equals the sum of their individual probabilities [Casella and Berger, 2002, Definition 1.2.4]. (“Countably infinitely many” means “as many as there are integer numbers”.)
When the context that defines is obvious, often one suppresses explicit reference to it, as in this derivation: if denotes the negation of , then Convexity and the Addition Rule imply that because one but not both of and must be true.
The concept of independence pervades much of probability theory. Two propositions and are independent if the probability that both are true equals the product of their individual probabilities of being true. If asserts that there is a Queen in Alexandra’s poker hand, and asserts that Beatrice’s comprises red cards only, both hands having been dealt from the same deck, then and are independent. Intuitively, if knowledge of the truth of one proposition influences the assessment of probability of another, then they are dependent: in particular, two mutually exclusive propositions are dependent. If , then and are independent given .
When considering the probability of a proposition, it often proves advantageous to consider the truth or falsity of another one, somehow related to the first [Lindley, 2006, §5.6]. To assess the probability of a positive tuberculin skin test (§3.6), it is convenient to consider how the test performs separately in persons infected or not infected with Mycobacterium tuberculosis: if denotes infection, then , where is the probability of a false positive, and is the probability of a false negative, both more accessible than .
If an ideal reasoning agent (human or machine) assigns probabilities to events or to the truth of propositions according to the foregoing axioms, then this agent’s beliefs are said to be coherent. In these circumstances, if probabilities are used to inform bets concerning the truth of propositions in the universe of discourse where these probabilities are meaningful, then it is impossible (for a “bookie”) to devise a collection of bets that bring an assured loss to this agent (a so-called “Dutch Book”).
Now, suppose that, having ascertained the truth of a proposition , one produces as assessment of ’s truth on the evidence provided by . Next, one determines that , too, is true and revises this last assessment of ’s truth to become . The process whereby probabilities are updated is coherently extensible if the resulting assessment is the same irrespective of whether the evidence provided by and is brought to bear either sequentially, as just considered, or simultaneously. The incorporation of information from multiple sources, and the corresponding propagation of uncertainty, that is carried out by application of Bayes’ formula, which is described next and illustrated in examples §3.6 and §6.7, is coherently extensible.
If exactly one (that is, one and one only) among propositions can be true, and is another proposition with positive probability, then
| (1) |
This follows from the axioms above because (Multiplication axiom), whose numerator equals (Multiplication axiom), and whose denominator equals (“extending the conversation”, as in §3.3).
Richard has been advised that his tuberculin skin test has returned a positive result. The tuberculin skin test has a reported false-negative rate of during the initial evaluation of persons with active tuberculosis [American Thoracic Society, 1999, Holden et al., 1971]: this means that the probability is 0.25 that the test will yield a negative () response when administered to an infected person (), . Therefore, the probability is only 0.75 that infection will yield a positive test result. In populations where cross-reactivity with other mycobacteria is common, the test’s false-positive rate is 5%: that is, the conditional probability of a positive result () for a person that is not infected () is .
Richard happens to live in an area where tuberculosis has a prevalence of . Given the positive result of the test he underwent, the probability that he is infected is
Common sense suggests that the diagnostic value of the test should depend on its false-negative and false-positive rates, as well as on the prevalence of the disease: Bayes’ formula states exactly how these ingredients should be combined to produce , which expresses that diagnostic value quantitatively.
Richard has the tuberculin skin test repeated, and this second test also turns out positive. To incorporate this additional piece of evidence into the probability that Richard is infected, first we summarize the state of knowledge (about whether he is infected) determined by the result from the first test. This is done by defining and , and using them in the role that the overall probability of infection () or non-infection () played prior to Richard’s first test, when all one knew about his condition was that he was a member of a population where the prevalence of tuberculosis was .
Again applying Bayes’ theorem, and assuming that the two tests are independent, the revised probability that Richard is infected after two positive tests is
If, instead, one had been initially told that Richard had had two independent, positive tuberculin skin tests, then the calculation would have been:
This example illustrates the fact that Bayes’ theorem produces the same probability irrespective of whether the information is incorporated sequentially, or all at once.
The example in §3.6 illustrated how the probability of Richard being infected increased (relative to the overall probability of infection in the town where he lives) as a first, and then a second tuberculin test turned out positive. However, even if he is infected, by chance alone a test may turn out negative. In a sequence of tests, therefore, the probability of his being infected may oscillate, increasing when a test turns out positive, decreasing when some subsequent test turns out negative.
Therefore, the question naturally arises of whether a person employing the Bayesian method of exploiting information, and incorporating it into the current state of knowledge, ever will, in situations of uncertainty, arrive at conclusions with overwhelming confidence. Jimmie Savage proved rigorously that the answer is “yes” with great generality: “with observation of an abundance of relevant data, the person is almost certain to become highly convinced of the truth, and […] he himself knows this to be the case” [Savage, 1972, §3.6].
The restriction to “relevant data” is critical: in relation with the tuberculin test, if it happened that , then the test would have no discriminatory power, and in fact would be irrelevant to learning about disease status.
The notion of random variable originates in games of chance, like roulette, whose outcomes are unpredictable. Its rigorous mathematical definition (measurable function from one probability space into another) is unlikely to be of great interest to the metrologist. Instead, one may like to keep in mind its heuristic meaning: the value of a quantity that has a probability distribution as an attribute whose role is to describe the uncertainty associated with that value.
In the version of roulette played in Monte Carlo, the possible outcomes are numbers in the set (usually one disregards other possible, but “uninteresting” outcomes, including those where the ball exits the wheel and lands elsewhere, or where it lands inside the wheel but in none of its numbered pockets). Once those 37 numbers are deemed to be equally likely, one can speak of a random variable that is equal to with probability , or that is odd with probability . (Note that these statements are meaningful irrespective of whether the event in question will happen in the future, or has happened already, provided one does not know its actual outcome yet).
The GE A19 Party Light 25 W incandescent light bulb has expected lifetime 2000 h: this is usually taken to mean that, if a brand new bulb is turned on and left on supplied with constant 120 V electrical current until it burns out, its actual lifetime may be described as a realized value (realization, or outcome) of a random variable with an exponential probability distribution (§4.10) whose expected value is — this is denoted in §4.10, and in general it needs to be estimated from experimental data.
The concept of random variable applies just as well to domains of discourse unrelated to games of chance, hence can be used to suggest uncertainty about the value of a quantity, irrespective of the source of this uncertainty, including situations where there is nothing “random” (in the sense of “chancy”) in play.
For the most part, upper case letters (Roman or Greek) denote generic quantity values modeled as random variables, and their lowercase counterparts denote particular values.
Upper case letters like or , and , denote generic random variables, without implying that any of the former necessarily play the role of input quantity values (as defined in the international vocabulary of metrology (VIM) Joint Committee for Guides in Metrology [2008c], VIM 2.50), or that the latter necessarily plays the role of output quantity values (VIM 2.51) in a measurement model (VIM 2.48).
The probabilities most commonly encountered in metrological practice concern sets of numbers that a quantity value may take: in this case, if denotes a random variable whose values belong to a set , and is a subset of , then denotes the probability that ’s value lies in . For example, if represents the length (expressed in meter, say) of a gauge block, then would be the set of all possible values of length, and could be the subset of such values between 0.0423 m and 0.0427 m, say.
Given a random variable one can then define a function such that for all to which a probability can be assigned. This is called ’s probability distribution.
If is countable (that is, either finite or infinite but with as many elements as there are positive integers), then one says that has a discrete distribution, which is fully specified by the probability it assigns to each value in . For example, the outcome of a roulette wheel is a random variable whose probability distribution is discrete.
If is uncountable (that is, it has as many elements as there are real numbers) and for all , then one says that has a continuous distribution. For example, the lifetime of an incandescent light bulb that does light up and then is constantly left on until it burns out is a random variable with a continuous distribution.
A distribution may be neither discrete nor continuous, but of a mixed type instead: for example, when a random variable is equal to 0 with probability , and has an exponential distribution (see §4.10) with probability . Since a brand new light bulb has a positive probability of burning out the instant it is turned on, its lifetime may more realistically be modeled as a random variable that has an “atom” of probability at 0, and is exponential with the complementary probability.
The probability distribution of a random variable whose possible values are real numbers, can be succinctly described by its probability distribution function, which is the function such that for every real number .
Note that the symbol we use here to denote the probability distribution function, is the same that we used in §4.5 to denote the probability distribution itself. Any confusion this may cause will be promptly resolved by examining the argument of : if it is a set, then we mean the distribution itself, while if it is a number or a vector with numerical components, then we mean the probability distribution function.
For example, if is real-valued and is a particular real number, then in the on the left hand side refers to the probability distribution function, while the on the right hand side refers to the distribution itself because denotes the set of all real numbers no greater than . Since the distribution function determines the distribution, the confusion is harmless.
If has a discrete distribution (§4.5), then its probability density (also known as its probability mass function) is the function such that for .
If is uncountable and ’s distribution is continuous and sufficiently smooth (in the sense described next), then the corresponding probability density function (PDF) is defined similarly to a material object’s mass density, as follows.
Consider the simplest case, where is an interval of real numbers, and suppose that is one point in the interior of this interval. Now suppose that is an infinite sequence of positive numbers decreasing to zero. If ’s probability distribution is sufficiently smooth, then the limit exists. The function so defined is ’s probability density function. If the distribution function is differentiable, then the probability density is the derivative of the probability distribution function, .
Both the probability distribution function and the probability density function have multivariate counterparts.
The expectation (expected value, or mean value) of a (scalar or vector valued) function of a random variable is if has a continuous probability distribution with density , or if has a discrete distribution. Note that can be computed without determining the probability distribution of the random variable explicitly.
indicates ’s location, or the center of its probability distribution: therefore it is a most succinct summary of this distribution, and it is the best estimate of ’s value in the sense that it has the smallest mean squared error.
The median is another indication of location for a scalar random variable: it is any value such that and , and it need not be unique. The median is the best estimate of ’s value in the sense that it has the smallest absolute deviation.
Neither the mean nor the median need be “representative” values of the distribution. For example, when denotes a proportion whose most common values are close to 0 or to 1 and its mean is close to ½, then values close to the mean are very unlikely. need not exist (in the sense that the defining integral or sum may fail to converge).
, where is a positive integer, is called ’s th moment. The variance of is , or, equivalently, the difference between its second moment and the square of its first moment. The positive square root of the variance, , is the standard deviation of .
The only values that a Poisson distributed random variable can take are the non-negative integers: 0, 1, 2, …, and the probability that its value is is , where is some given positive number, and . This model distributes its unit of probability into infinitely many lumps, one at each non-negative integer, so that decreases rapidly with increasing , and . Both the expected value and the variance equal . The number of alpha particles emitted by a sample containing the radionuclide , during a period of seconds that is a small fraction of this isotope’s half-life (138 days), is a value of a Poisson random variable with mean proportional to .
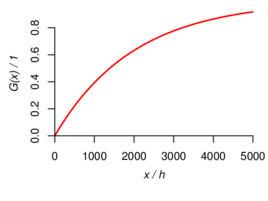
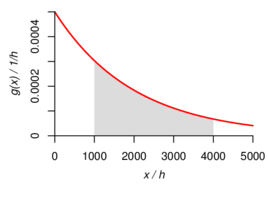
Suppose that represents the lifetime (thousands of hours) of an incandescent light bulb, such that, for , , for some given number : note that, as decreases toward 0, and increases without limit, approaches 1. Focus on a particular number , and consider the ratio for some . As decreases to this ratio approaches . Therefore, the function such that is the probability density of the exponential distribution. In this case, the probability distribution function is such that . ’s mean value is , and its variance is . Figure 1 illustrates both the distribution function and the density for the case where .


Suppose that represents a bivariate quantity value, for example, the Cartesian coordinates of a point inside a circle of unit radius centered at . In this case the range of is this unit circle. The joint probability distribution of and describes a state of knowledge about the location of : for example, that more likely than not is less than ½ away from the center of the circle: statements of this kind involve and together (that is, jointly).
The marginal probability distributions of and are the probability distributions that characterize the state of knowledge about each of them separately from the other: for example, that more likely than not , irrespective of .
Clearly, the marginal distributions have to be consistent with the joint distribution, and while it is true that the joint distribution determines the marginal distributions, the reverse is not true, in that typically there are many joint distributions consistent with given marginal distributions [Possolo, 2010].
Now, suppose one knows that . This implies that , hence that is somewhere on a particular chord of the unit circle. The conditional probability distribution of given that is a (univariate) probability distribution over this chord.
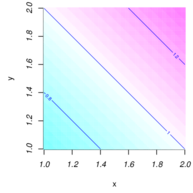
The random variables and take values in the interval and have joint probability density function such that for and is zero otherwise (Figure 2): since and , is a bona fide (bivariate) probability density.
The density of the marginal distribution of is , and similarly for . And the density of the conditional distribution of given is .
To determine the probability density of , also depicted in Figure 2, note that . First, consider the case : and . Next, consider the case : and .
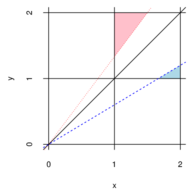
The (scalar or vectorial) random variables and are independent if and only if for all subsets and in their respective ranges (to which probabilities can be coherently assigned.) Suppose and have joint probability distribution with probability density function , and marginal density functions and : the random variables are independent if and only if .
Suppose that the probability distribution of a point is uniform inside the circle of unit radius centered at the origin of the Euclidean plane. This means that the probability that a point with Cartesian coordinates should lie in a subset of this circle is proportional to ’s area, but is otherwise independent of ’s shape or location within the circle. The probability density function of the joint distribution of and is the function such that if , and otherwise. The random variables and are dependent (§4.13): for example, if one is told that , then one can surely conclude that . The marginal distribution of has density such that for . has expected value 0 and standard deviation ½. Owing to symmetry, and have identical marginal distributions.
If two or more of the random variables are dependent, then modeling their individual probability distributions will not suffice to specify their joint behavior: their joint probability distribution is needed.
One commonly used metric of dependence between two random variables and is Pearson’s product-moment correlation coefficient, defined as . However, it is possible for the variables to be dependent and still have .
When the only information in hand are the expected values, standard deviations, and correlations, and still one needs a joint distribution consistent with this information, then the usual course of action is to assign distributions to them individually, and then manufacturing a joint distribution using a copula [Possolo, 2010] — there is, however, a multitude of different copulas that can be used for this purpose, and the choice that must be made generally is influential.
If a random variable is a function of other random variables, , then and the joint probability distribution of determine the probability distribution of .
If only the means, standard deviations, and correlations of are known, then it still is possible to derive approximations to the mean and standard deviation of , by application of the Delta Method.
If the joint probability distribution of is known, then it may be possible to determine the probability distribution of analytically, using the change of variables formula.
In general, it is possible to obtain a sample from ’s distribution by taking a sample from the joint distribution of and applying to each element of this sample (§5.8). The results may then be summarized in several different ways: one of them is an estimate of the probability density of [Silverman, 1986], a procedure that is implemented in function density of the R environment for statistical programming and graphics [R Development Core Team, 2010].
If is a random variable with mean and variance , is a differentiable real-valued function of a real variable whose first derivative does not vanish at , and , then , and . (This results from the so-called Taylor approximation that replaces by a straight line tangent to its graph at .)
If is an average of independent, identically distributed random variables with finite variance, then also is approximately Gaussian with mean and standard deviation , where denotes the absolute value of the first derivative of evaluated at . The quality of the approximation improves with increasing .
When and exists and is not zero, is an average of independent, identically distributed random variables with finite variance, and is large, then the probability distribution of is approximately like that of , where denotes a Gaussian (or, normal) random variable with mean 0 and standard deviation 1. Since the variance of is 2, the standard deviation of is approximately , rather different from what applies in the conditions of §5.2.
Consider a surface whose reflectance is Lambertian: that is, light falling on it is scattered in such a way that the surface’s brightness apparent to an observer is the same regardless of the observer’s angle of view. The radiant power emitted by such surface that is measured by a sensor aimed at angle to the surface’s normal is proportional to , hence one writes [Cannon, 1998, Köhler, 1998].
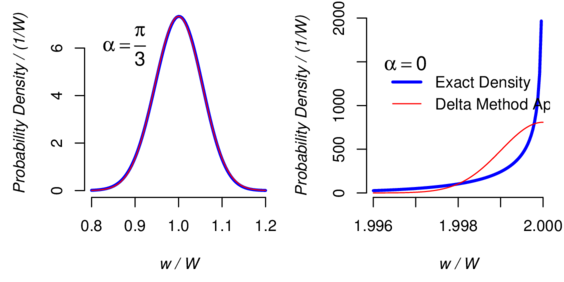
If knowledge about the value of is modeled by a Gaussian distribution with mean and standard measurement uncertainty (both expressed in radians), then §5.2 (with ) suggests that knowledge of should be described approximately by a Gaussian distribution with mean and standard measurement uncertainty .
If, for example, , , and , then the approximation to ’s distribution that the Delta Method suggests, of a Gaussian distribution with mean and standard deviation , is remarkably accurate (Figure 3).
When the detector is aimed squarely at the target, that is , this approximation no longer works because the first derivative of the cosine vanishes at , which is the degenerate case that §5.3 contemplates. In this case, ’s standard measurement uncertainty is approximately . For and , this equals , which is accurate to the two significant digits shown. However, Figure 3 shows that, in this case, the Delta Method produces a poor approximation.
When , the probability density of is markedly asymmetrical, and the meaning of ’s standard deviation is rather different from its meaning when . Indeed, when the probability that should lie within one standard deviation of its expected value is approximately.
The Delta Method can be extended to apply to a function of several random variables. Suppose that , …, are averages of sets of random variables whose variances are finite. The variables in each set are independent and identically distributed, those in set having mean and variance . However, variables in different sets may be dependent, hence the may be dependent, too. Let denote the symmetrical matrix whose element is the covariance between and , for .
Now, consider the random variable , where denotes a real-valued function of variables whose first partial derivatives are continuous and none vanishes at . If is finite, then also is approximately Gaussian with mean and variance .
If are uncorrelated and have means and standard deviations , then the Delta Method approximation reduces to a well-known formula first presented by Gauss [Gauss, 1823, §18, Problema]: , where the sensitivity coefficient is the value at of the th partial derivative of with respect to .
If a beam of monochromatic light of power (W) travels a path of length (m) through a solution containing a solute whose molar absorptivity for that light is (L mol-1 m-1), and whose molar concentration is (mol L-1), then the beam’s power is reduced to (W) such that . Application of Gauss’s formula (§5.5) to yields:
Darcy’s law relates the dynamic viscosity of a fluid to the volumetric rate of discharge (volume per unit of time) when the fluid flows through a permeable cylindrical medium of cross-section and intrinsic permeability under a pressure drop of along a length , as follows: .
To compute an approximation to the standard deviation of , one may use the formula from §5.5 directly, or first take the logarithm of both sides, which linearizes the relationship, . Applied to these logarithms, the formula from §5.5 is exact. The approximation is then done for each term separately, using the univariate Delta Method.
Since , and similarly for the other logarithmic terms, . In other words, the square of the coefficient of variation of is approximately equal to the sum of the squares of the variation coefficients of the other variables.
The Monte Carlo method offers several important advantages over the Delta Method described in §5.2 and §5.5: (i) it can produce as many correct significant digits in its results as may be required; (ii) it does not involve the computation of derivatives, either analytically or numerically; (iii) it is applicable in many situations where the Delta Method is not; (iv) it provides a picture of the whole probability distribution of a function of several random variables, not just an approximation to it, or to its mean and standard deviation.
The Monte Carlo method in general dates back to the middle of the twentieth century [Metropolis and Ulam, 1949, Metropolis et al., 1953]. A variant used in mathematical statistics is known as the parametric bootstrap [Efron and Tibshirani, 1993]. This involves using random draws from a (possibly multivariate) probability distribution whose parameters have been replaced by estimates thereof (for example, means of posterior probability distributions, §6) to ascertain the probability distribution of a function of one (or more) random variables. Morgan and Henrion [1992] and Joint Committee for Guides in Metrology [2008b] describe how it may be employed to evaluate measurement uncertainty, and provide illustrative examples.
The procedure comprises the following steps:
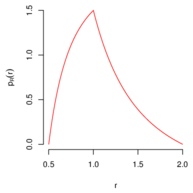
The radius and the height of a cylinder are values of independent random variables with exponential probability distributions with mean 1 m. To characterize the probability distribution of its volume , draw a sample of size from the joint distribution of and , and compute the volume corresponding to each pair of sampled values to obtain a sample of the same size from the distribution of . The average and standard deviation of these values are 6.3 m3 and 21 m3, and they are estimates (whose two most significant digits are exact) of the mean and standard deviation of . Figure 4 depicts an estimate of the corresponding probability density.
Suppose that is a random variable with a continuous distribution and values in , with probability distribution function and probability density function , and consider the random variable where denotes a real-valued function of a real variable. Let denote the set where takes its values, and let and denote ’s probability distribution function and probability density function, respectively. In these circumstances [Casella and Berger, 2002, Chapter 2].
A horizontal beam of light emerges from a tiny hole in a wall and travels along a 1 m long path at right angles to the wall, towards a flat mirror that oscillates freely around a vertical axis. When the mirror’s surface normal makes an angle with the beam, its reflection hits the wall at distance from the hole (positive to the right of the hole and negative to the left). If is uniformly (or, rectangularly) distributed between and , then , and ’s probability density is such that for . As it turns out, both the mean and the standard deviation of are infinite [Feller, 1971, Page 51].
Suppose that are random variables and consider for , and where are real-valued functions of real variables each.
Suppose also that (i) the vector takes values in an open subset of -dimensional Euclidean space, and has a continuous joint probability distribution with probability density function ; (ii) the vector-valued function is invertible, and the inverse has a Jacobian determinant that does not vanish on .
| (2) |
Note that is a scalar, and denotes its absolute value.
Suppose that and are independent, Gaussian random variables with mean 0 and variance 1, and let , and , for given real numbers and . The inverse transformation maps onto , and has Jacobian determinant whose absolute value is . Since the density of the joint probability distribution of and is , application of the multivariate change-of-variable formula yields
But this means that and also are independent and Gaussian with mean 0 and variance . On the one hand, this result is surprising because and both are functions of the same random variables. On the other hand it is hardly surprising because the transformation amounts to a rotation of the coordinate axes, followed by a global dilation. Since the joint distribution of and is circularly symmetric relative to , so will the joint distribution of and be, which implies independence and the same functional form for the density, up to a difference in scale.
To compute the probability density of the ratio of two independent and exponentially distributed random variables and with mean , define the function such that , whose inverse is , with Jacobian determinant . The multivariate change-of-variable formula then yields for the density of the joint distribution of and . The (marginal) density of is , for , being 0 otherwise.
indeed is a probability density function because it is a non-negative function and . However, since , neither the mean nor the variance of is finite. The Delta Method, however, would have suggested that and that the coefficient of variation (ratio of the standard deviation to the mean) of is approximately.
The inverse of the transformation that maps the polar coordinates of a point in the Euclidean plane to its Cartesian coordinates is such that for and , with Jacobian determinant . If and are independent Gaussian random variables with mean 0 and variance 1, then the probability density of is . Since , it follows that and are independent, the former having a Rayleigh distribution with mean , the latter a uniform distribution between and .
The statistical inferences we are primarily interested in are probabilistic statements about the unknown value of a quantity, produced by application of a statistical method. In the example of §6.6, one of the inferences is this statement: the probability is 95% that the difference between the numbers of hours gained with the two soporifics is between 0.7 h and 2.5 h.
Another common inference is an estimate of the value of a quantity, which must be qualified with an assessment of the associated uncertainty. In the example of §6.8, a typical inference of this kind would be this: the difference in mean levels of thyroxine in the serum of two groups of children diagnosed with hypothyroidism is estimated as with standard uncertainty (Figure 6).
In our treatment of this example, the inference is based entirely on a small set of empirical data, and on a particular choice of statistical model used to describe the dispersion of the data, and to characterize the fact that no knowledge other than the data was brought into play.
Statistical methods different from the one we used could have been employed: some of these would produce the same result (in particular those illustrated when this dataset was first described [Student, 1908, Fisher, 1973]), while others would have produced different results.
Even when the result is the same, it may be variously interpreted:
Bayesian inference [Bernardo and Smith, 2000, Lindley, 2006, Robert, 2007] is a class of statistical procedures that serve to blend preexisting information about the value of a quantity with fresh information in empirical data.
The defining traits of a Bayesian procedure are these:
Let denote the value of the quantity of interest, which we model as realized value of a random variable with probability density function that encodes the state of knowledge about prior to obtaining fresh data, and which must be defined even if there is no prior knowledge.
Defining such often is a challenging task. If in fact there exists substantial prior knowledge about , then it needs to be elicited from experts in the matter and encapsulated in the form of a particular probability density: Garthwaite et al. [2005] review how this may be done. For example, when measuring the mass fraction of titanium in a mineral specimen, then knowledge of the species (ilmenite, titanite, rutile, etc.) of the specimen is highly informative about that mass fraction. Familiarity with the process of analytical chemistry employed to make the measurement may indicate the dispersion of values to be expected.
In some cases, essentially no prior knowledge exists about , or none is deemed reliable enough to be taken into account. In such cases, a so-called non-informative prior distribution needs to be produced and assigned to that reflects this state of affairs: if is univariate (that is, a single number), then the rules developed by Jeffreys [1961] often prove satisfactory; if is multivariate (that is, a numerical vector), then the so-called reference prior distributions are recommended [Bernardo and Smith, 2007] (these reduce to Jeffreys’s in the univariate case).
These rules often produce a that is improper, in the sense that diverges to infinity, where denotes the range of . (If should have a discrete distribution then this integral is replaced by a sum.) Fortunately, once used in Bayes Rule (§3.5 and §6.4), improper priors often lead to proper posterior probability distributions.
The empirical data (which may be a single number, a numerical vector, or a data structure of still greater complexity) are modeled as realized values of a random variable whose probability density describes the corresponding dispersion of values.
This density must depend on , which is another way of saying that the data are informative about (otherwise there would be nothing to be gained by observing them). In fact, this is the density of the conditional probability distribution of given that . Choosing a specific functional form for it generally is a non-trivial exercise: it involves defining a statistical model that correctly captures the dispersion of values likely to be obtained in the experiment that produces them.
Once the data are in hand, becomes a function of alone, being largest for values of that make the data appear most likely. As such, it still is non-negative, but its integral (or sum, if ’s distribution should be discrete) over the range of , need not be 1.
Suppose that both given that and have continuous distributions with densities and . In these circumstances, Bayes rule becomes
| (3) |
The function , which is defined over the range of for each fixed value , is the density of the posterior distribution of the value of the quantity of interest given the data.
In some cases this can be computed in closed form, in many others it cannot. In all cases it is possible to obtain a sample from this posterior distribution by application of a procedure known as Markov Chain Monte Carlo (MCMC) [Gelman et al., 2003]. This sample can then be summarized as described in §5.8.
Once infected by influenza A virus, an epithelial cell of the upper respiratory tract releases virions on average, which may then go on to infect other cells. This number depends on the volume of the cell, and we will treat it as realized value of a non-observable random variable with an exponential distribution whose expected value, for some , is known. Given , the actual number of virions that are released is , and this is like a realized value of a Poisson random variable with mean .
Suppose that the prior density is , and the likelihood function is , for . The posterior distribution of given belongs to the gamma family, and has expected value , variance , and density
The differences between the numbers of additional hours of sleep that ten patients gained when using two soporific drugs, described in examples given by Student [1908] and [Fisher, 1973, §24], were 1.2 h, 2.4 h, 1.3 h, 1.3 h, 0.0 h, 1.0 h, 1.8 h, 0.8 h, 4.6 h, and 1.4 h.
Suppose that, given and , these are realized values of independent Gaussian random variables with mean and variance . Let denote their average, and denote the sum of their squared deviations from divided by 9. In these circumstances, the likelihood function is .
Assume, in addition, that and are realized values of non-observable random variables and that are independent a priori and such that and are uniformly distributed between and (both improper prior distributions). Then, given and , is like a realized value of a random variable with a Student’s distribution with degrees of freedom, and is like a realized value of a random variable with a chi-squared distribution with degrees of freedom [Box and Tiao, 1973, Theorem 2.2.1].
Therefore, the expected value of the posterior distribution of the mean difference of hours of sleep gained is , and the standard deviation is . A 95 % probability interval for ranges from 0.7 h to 2.5 h, and a similar one for ranges from 0.8 h to 2.2 h.
Suppose that and are the counterparts of and once the information in the data has been taken into account: that is, their probability distribution is the joint (or, bivariate) posterior probability distribution given the data. Even though and were assumed to be independent a priori, and turn out to be dependent a posteriori (that is, given the data), but their correlation is zero [Lindley, 1965b, §5.4].
A major hurricane has category 3, 4, or 5 on the Saffir-Simpson Hurricane Scale [Simpson, 1974]: its central pressure is no more than 945 mbar (94 500 Pa), it has winds of at least (49.6 m s-1), generates sea surges of 9 feet (2.7 m) or greater, and has the potential to cause extensive damage.
The numbers of major hurricanes that struck the U.S. mainland directly, in each decade starting with 1851–1860 and ending with 1991–2010, are: 6, 1, 7, 5, 8, 4, 7, 5, 8, 10, 8, 6, 4, 4, 5, 7 [Blake et al., 2011]. Let denote the number of decades, denote the corresponding counts, and . Suppose that one wishes to predict , the number of such hurricanes in the decade 2011–2020.
Assume that the mean number of such hurricanes per decade will have remained constant between 1851 and 2010 (certainly a questionable assumption), with unknown value , and that, conditionally on this value, , …, , and are realized values of independent Poisson random variables , …, (observable), (non-observable), all with mean value : their common probability density is for . This model is commonly used for phenomena that result from the cumulative effect of many improbable events [Feller, 1968, XI.6b].
Even though the goal is to predict , the fact that there is no a priori knowledge about other than that it must be positive, requires that this be modeled as the (non-observable) value of a random variable whose probability distribution must reflect this ignorance. (According to the Bayesian paradigm, all states of knowledge, even complete ignorance, have to be modeled using probability distributions.)
If the prior distribution chosen for is the reference prior distribution [Berger, 2006, Bernardo, 1979, Bernardo and Smith, 2000], then the value of its probability density at should be proportional to [Bernardo and Smith, 2000, A.2], an improper prior probability density. However, the corresponding posterior distribution for is proper, in fact it is a gamma distribution with expected value and probability density function such that
| (4) |
However, what is needed for the aforementioned prediction is the conditional distribution of given the observed counts: the so-called predictive distribution [Schervish, 1995, Page 18]. If denotes the corresponding density, then
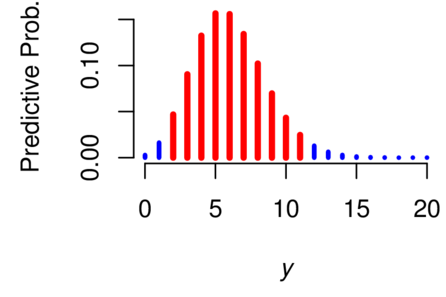
This defines a discrete probability distribution on the non-negative integers, often called a Poisson-gamma mixture distribution [Bernardo and Smith, 2000, §3.2.2]. For our data, since achieves a maximum at (Figure 5), this is the (a posteriori) most likely number of major hurricanes that will hit the U.S. mainland in 2011–2020. The mean of the posterior distribution is . Since the probability is 0.956 that ’s value lies between 2 and 11 (inclusive), the interval whose end-points are 2 and 11 is a coverage interval for .
[Altman, 1991, Table 9.6] lists measurement results from Hulse et al. [1979], for the concentration of thyroxine in the serum of sixteen children diagnosed with hypothyroidism, of which nine had slight or no symptoms, and the other seven had marked symptoms. The values measured for the former, all in units of nmol/L, were 34, 45, 49, 55, 58, 59, 60, 62, and 86; and for the latter they were 5, 8, 18, 24, 60, 84, and 96. The averages are and , and the standard deviations are and .
Our goal is to produce a probability interval for the difference between the corresponding means, and , say, when nothing is assumed known a priori either about these means or about the corresponding standard deviations, and , which may be different.
Given the values of these four parameters, suppose that the values measured in the children with slight or no symptoms are observed values of independent Gaussian random variables with common mean and standard deviation , and that those measured in the children with marked symptoms are observed values of independent Gaussian random variables , also independent of the , with common mean and standard deviation .
The problem of constructing a probability interval for under these circumstances is known as the Behrens-Fisher problem [Ghosh and Kim, 2001]. For the Bayesian solution, we regard , , and as realized values of non-observable random variables , , , and , assumed independent a priori and such that , , , and all are uniformly distributed over the real numbers (hence have improper prior distributions). The corresponding posterior distributions all are proper provided and . However, the density of the posterior probability distribution of given the data cannot be computed in closed form.
This problem in Bayesian inference, and other problems much more demanding than this, can be solved using the MCMC sampling technique mentioned in §6.4, for which there exist several generic software implementations: we obtained the results presented below using function metrop of the R package mcmc [Geyer, 2010]. Typically, all that is needed is the logarithm of the numerator of Bayes formula (3). Leaving out constants that do not involve , , or , this is
MCMC produces a sample of suitably large size from the joint posterior distribution of , , , and , given the data, say , …, . The 95 % probability interval for the difference in mean levels of thyroxine in the serum of the two groups, which extends from to , and Figure 6, are based on a sample of size . The probability density in this figure, and that probability interval, were computed as described in MC4.c and MC4.d of §5.8, only applied to the differences .
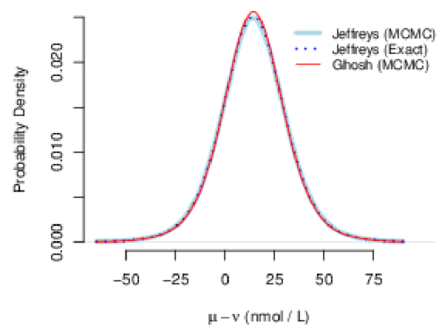
In this particular case it is possible to ascertain the correctness of the results owing to an interesting, albeit surprising result: the posterior means are independent a posteriori, and have probability distributions that are re-scaled, shifted versions of Student’s distributions with and degrees of freedom [Box and Tiao, 1973, 2.5.2]. Therefore, by application of the Monte Carlo method of §5.8, one may obtain a sample from the posterior distribution of the difference independently of the MCMC procedure: the results are depicted in Figure 6 (where they are labeled “Jeffreys (Exact)”), and are essentially indistinguishable from the results of MCMC.
This same figure shows yet another posterior density that differs hardly at all from the posterior density corresponding to Jeffreys’s prior: this alternative result corresponds to the “matching” prior distribution (also improper) derived by Ghosh and Kim [2001], whose density is proportional to . This illustrates a generally good practice: that the sensitivity of the results of Bayesian analysis should be evaluated by comparing how they vary when different but comparably acceptable priors are used.
Antonio Possolo thanks colleagues and former colleagues from the Working Group 1 of the Joint Committee for Guides in Metrology, who offered valuable comments and suggestions in multiple discussions of an early draft of a document that he had submitted to the consideration of this Working Group and that included material now in the present document: Walter Bich, Maurice Cox, René Dybkær, Charles Ehrlich, Clemens Elster, Tyler Estler, Brynn Hibbert, Hidetaka Imai, Willem Kool, Lars Nielsen, Leslie Pendrill, Lorenzo Peretto, Steve Sidney, Adriaan van der Veen, Graham White, and Wolfgang Wöger. Antonio Possolo is particularly grateful to Tyler Estler for suggestions regarding §2.3 and §3.1, and to Graham White for suggestions and corrections that greatly improved §3.6, on the tuberculin test. Both authors thank their common NIST colleagues Andrew Rukhin and Jack Wang for suggesting many corrections and improvements. Mary Dal-Favero and Alan Heckert, both from NIST, kindly facilitated the deployment of this material on the World Wide Web.
D. G. Altman. Practical Statistics for Medical Research. Chapman & Hall/CRC, Boca Raton, FL, 1991. Reprinted 1997.
American Thoracic Society. Diagnostic standards and classification of tuberculosis in adults and children. American Journal of Respiratory and Critical Care Medicine, 161:1376–1395, 1999.
J. Berger. The case for objective Bayesian analysis. Bayesian Analysis, 1(3):385–402, 2006. URL http://ba.stat.cmu.edu/.
J. Bernardo and A. Smith. Bayesian Theory. John Wiley & Sons, New York, 2000.
J. Bernardo and A. Smith. Bayesian Theory. John Wiley & Sons, Chichester, England, 2nd edition, 2007.
J. M. Bernardo. Reference posterior distributions for Bayesian inference. Journal of the Royal Statistical Society, 41:113–128, 1979.
E. S. Blake, C. W. Landsea, and E. J. Gibney. The deadliest, costliest, and most intense United States tropical cyclones from 1851 to 2010 (and other frequently requested hurricane facts). Technical Report Technical Memorandum NWS NHC-6, NOAA, National Weather Service, National Hurricane Center, Miami, Florida, August 2011.
L. Bovens and W. Rabinowicz. Democratic answers to complex questions — an epistemic perspective. Synthese, 150:131–153, 2006.
G. E. P. Box and G. C. Tiao. Bayesian Inference in Statistical Analysis. Addison-Wesley, Reading, Massachusetts, 1973.
T. W. Cannon. Light and radiation. In C. DeCusatis, editor, Handbook of Applied Photometry, chapter 1, pages 1–32. Springer Verlag, New York, New York, 1998.
R. Carnap. Logical Foundations of Probability. University of Chicago Press, Chicago, Illinois, 2nd edition, 1962.
G. Casella and R. L. Berger. Statistical Inference. Duxbury, Pacific Grove, California, 2nd edition, 2002.
N. Clee. Who’s the daddy of them all? In Observer Sport Monthly. Guardian News and Media Limited, Manchester, UK, Sunday March 4, 2007.
R. T. Clemen and R. L. Winkler. Combining probability distributions from experts in risk analysis. Risk Analysis, 19:187–203, 1999.
R. T. Cox. Probability, frequency and reasonable expectation. American Journal of Physics, 14:1–13, 1946.
R. T. Cox. The Algebra of Probable Inference. The Johns Hopkins Press, Baltimore, Maryland, 1961.
A. C. Davison and D. Hinkley. Bootstrap Methods and their Applications. Cambridge University Press, New York, NY, 1997.
B. de Finetti. La prévision: ses lois logiques, ses sources subjectives. Anales de l’Institut Henri Poincaré, 7:1–68, 1937.
B. de Finetti. Theory of Probability: A critical introductory treatment. John Wiley & Sons, Chichester, 1990. Two volumes, translated from the Italian and with a preface by Antonio Machì and Adrian Smith, with a foreword by D. V. Lindley, Reprint of the 1975 translation.
M. H. DeGroot. A conversation with Persi Diaconis. Statistical Science, 1(3):319–334, August 1986.
M. H. DeGroot and M. J. Schervish. Probability and Statistics. Addison-Wesley, 4th edition, 2011.
P. Diaconis and D. Ylvisaker. Quantifying prior opinion. In J. M. Bernardo, M. H. DeGroot, D. V. Lindley, and A. Smith, editors, Bayesian Statistics, volume 2, pages 163–175. North-Holland, Amsterdam, 1985.
F. W. Dyson, A. S. Eddington, and C. Davidson. A determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of May 29, 1919. Philosophical Transactions of the Royal Society of London, Series A, Containing Papers of a Mathematical or Physical Character, 220:291–333, 1920.
B. Efron and R. J. Tibshirani. An Introduction to the Bootstrap. Chapman & Hall, London, UK, 1993.
W. Feller. An Introduction to Probability Theory and Its Applications, volume I. John Wiley & Sons, New York, 3rd edition, 1968. Revised Printing.
W. Feller. An Introduction to Probability Theory and Its Applications, volume II. John Wiley & Sons, New York, 2nd edition, 1971.
R. A. Fisher. Statistical Methods for Research Workers. Hafner Publishing Company, New York, NY, 14th edition, 1973.
B. Fitelson. Likelihoodism, bayesianism, and relational confirmation. Synthese, 156(3):473–489, 2007.
P. H. Garthwaite, J. B. Kadane, and A. O’Hagan. Statistical methods for eliciting probability distributions. Journal of the American Statistical Association, 100:680–701, June 2005.
C. F. Gauss. Theoria combinationis observationum erroribus minimis obnoxiae. In Werke, Band IV . Könighlichen Gesellschaft der Wissenschaften, Göttingen, 1823.
A. Gelman, J. B. Carlin, H. S. Stern, and D. B. Rubin. Bayesian Data Analysis. Chapman & Hall / CRC, 2nd edition, 2003.
C. J. Geyer. mcmc: Markov Chain Monte Carlo, 2010. URL http://CRAN.R-project.org/package=mcmc. R package version 0.8.
M. Ghosh and Y.-H. Kim. The Behrens-Fisher problem revisited: A Bayes-Frequentist synthesis. The Canadian Journal of Statistics, 29(1): 5–17, March 2001.
D. Gillies. Philosophical Theories of Probability. Routledge, London, UK, 2000.
C. Glymour. Theory and evidence. Princeton University Press, Princeton, New Jersey, 1980.
A. Hájek. Interpretations of probability. In E. N. Zalta, editor, The Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab, Center for the Study of Language and Information, Stanford University, Stanford, California, 2007. URL http://plato.stanford.edu/archives/win2007/entries/probability-interpret/.
S. Hartmann and J. Sprenger. Judgment aggregation and the problem of tracking the truth. Synthese, pages 1–13, 2011. URL http://dx.doi.org/10.1007/s11229-011-0031-5.
P.G. Hoel, S. C. Port, and C. J. Stone. Introduction to Probability Theory. Houghton Mifflin, 1971a.
P.G. Hoel, S. C. Port, and C. J. Stone. Introduction to Statistical Theory. Houghton Mifflin, 1971b.
M. Holden, M. R. Dubin, and P. H. Diamond. Frequency of negative intermediate-strength tuberculin sensitivity in patients with active tuberculosis. New England Journal of Medicine, 285:1506–1509, 1971.
J. A. Hulse, D. Jackson, D. B. Grant, P. G. H. Byfield, and R. Hoffenberg. Different measurements of thyroid function in hypothyroid infants diagnosed by screening. Acta Pædiatrica, 68:21–25, 1979.
E. T. Jaynes. Probability Theory in Science and Engineering. Colloquium Lectures in Pure and Applied Science, No. 4. Socony Mobil Oil Company, Dallas, Texas, 1958.
E. T. Jaynes. Probability Theory: The Logic of Science. Cambridge University Press, Cambridge, UK, 2003. G. L. Bretthorst, Editor.
H. Jeffreys. Theory of Probability. Oxford University Press, London, 3rd edition, 1961. Corrected Impression, 1967.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Guide to the expression of uncertainty in measurement. International Bureau of Weights and Measures (BIPM), Sèvres, France, September 2008a. URL http://www.bipm.org/en/publications/guides/gum.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 100:2008, GUM 1995 with minor corrections.
Joint Committee for Guides in Metrology. Evaluation of measurement data — Supplement 1 to the “Guide to the expression of uncertainty in measurement” — Propagation of distributions using a Monte Carlo method. International Bureau of Weights and Measures (BIPM), Sèvres, France, 2008b. URL http://www.bipm.org/en/publications/guides/gum.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 101:2008.
Joint Committee for Guides in Metrology. International vocabulary of metrology — Basic and general concepts and associated terms (VIM). International Bureau of Weights and Measures (BIPM), Sèvres, France, 2008c. URL http://www.bipm.org/en/publications/guides/vim.html. BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP and OIML, JCGM 200:2008.
R. Köhler. Photometric and radiometric quantities. In C. DeCusatis, editor, Handbook of Applied Photometry, chapter 2, pages 33–54. Springer Verlag, New York, New York, 1998.
D. Lindley. Understanding Uncertainty. John Wiley & Sons, Hoboken, New Jersey, 2006.
D. V. Lindley. Introduction to Probability and Statistics from a Bayesian Viewpoint — Part 1, Probability. Cambridge University Press, Cambridge, UK, 1965a.
D. V. Lindley. Introduction to Probability and Statistics from a Bayesian Viewpoint — Part 2, Inference. Cambridge University Press, Cambridge, UK, 1965b.
D. V. Lindley. Reconciliation of probability distributions. Operations Research, 31(5):866–880, September-October 1983.
D. V. Lindley. Making Decisions. John Wiley & Sons, London, 2nd edition, 1985.
D. H. Mellor. Probability: A Philosophical Introduction. Routledge, New York, 2005.
N. Metropolis and S. Ulam. The Monte Carlo Method. Journal of the American Statistical Association, 44:335–341, September 1949.
N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, and E. Teller. Equations of state calculations by fast computing machines. Journal of Chemical Physics, 21:1087–1091, 1953.
M. G. Morgan and M. Henrion. Uncertainty — A Guide to Dealing with Uncertainty in Quantitative Risk and Policy Analysis. Cambridge University Press, New York, NY, first paperback edition, 1992. 10th printing, 2007.
P. A. Morris. Combining expert judgments: A bayesian approach. Management Science, 23(7):679–693, March 1977.
J. Neyman. Frequentist probability and frequentist statistics. Synthese, 36(1):97–131, 1977.
K. R. Popper. The propensity interpretation of probability. British Journal of the Philosophy of Science, 10:25–42, 1959.
A. Possolo. Copulas for uncertainty analysis. Metrologia, 47:262–271, 2010.
R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2010. URL http://www.R-project.org. ISBN 3-900051-07-0.
F. P. Ramsey. Truth and probability. In R.B. Braithwaite, editor, The Foundations of Mathematics and other Logical Essays, chapter VII, pages 156–198. Harcourt, Brace and Company, New York, 1999 electronic edition, 1926, 1931. URL http://homepage.newschool.edu/het/texts/ramsey/ramsess.pdf.
H. Reichenbach. The Theory of Probability: An Inquiry into the Logical and Mathematical Foundations of the Calculus of Probability. University of California Press, Berkeley, California, 1949. English translation of the 1935 German edition.
C. P. Robert. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation. Springer, New York, NY, second edition, 2007.
L. J. Savage. The Foundations of Statistics. Dover Publications, New York, New York, 1972.
M. J. Schervish. Theory of Statistics. Springer Series in Statistics. Springer Verlag, New York, NY, 1995.
B. W. Silverman. Density Estimation. Chapman and Hall, London, 1986.
R. H. Simpson. The hurricane disaster potential scale. Weatherwise, 27: 169–186, 1974.
M. Stone. The opinion pool. The Annals of Mathematical Statistics, 32: 1339–1342, December 1961.
Student. The probable error of a mean. Biometrika, 6(1):1–25, March 1908.
B. N. Taylor and C. E. Kuyatt. Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. National Institute of Standards and Technology, Gaithersburg, MD, 1994. URL http://physics.nist.gov/Pubs/guidelines/TN1297/tn1297s.pdf. NIST Technical Note 1297.
R. von Mises. Probability, Statistics and Truth. Dover Publications, New York, 2nd revised edition, 1981. ISBN 0486242145. Translation of the 3rd German edition.