

|
BINOMIAL PROPORTION TESTName:
The hypothesis test that the two binomial proportions are equal is
Dataplot computes this test for a number of different significance levels.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where you have raw data and want to perform a two-tailed test.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where you have raw data and want to perform a lower tailed test.
<SUBSET/EXCEPT/FOR qualification> where <y1> is the first response variable; <y2> is the second response variable; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax is used for the case where you have raw data and want to perform a upper tailed test.
where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; and <n2> is a parameter that specifies the sample size for sample 2. This syntax is used for the case where you have summary data and want to perform a two-tailed test.
where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; and <n2> is a parameter that specifies the sample size for sample 2. This syntax is used for the case where you have summary data and want to perform a lower tailed test.
where <p1> is a parameter that specifies the proportion of successes for sample 1; <n1> is a parameter that specifies the sample size for sample 1; <p2> is a parameter that specifies the proportion of successes for sample 2; and <n2> is a parameter that specifies the sample size for sample 2. This syntax is used for the case where you have summary data and want to perform an upper tailed test.
BINOMIAL PROPORTION TEST P1 N1 P2 N2
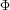 (Z) where (Z) where
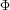 is the
cumulative distribution function for the standard normal distribution. is the
cumulative distribution function for the standard normal distribution.
For a lower tailed test, the p-value is equal to STATCDF. For an upper tailed test, the p-value is equal to 1 - STATCDF. For a two-tailed test, the p-value is equal to 2*(1 - STATCDF).
Ryan (2008), "Modern Engineering Statistics", Wiley, pp. 124-126.
LET X1 = 32
LET N1 = 38
LET P1 = X1/N1
LET X2 = 39
LET N2 = 44
LET P2 = X2/N2
SET WRITE DECIMALS 5
BINOMIAL PROPORTION TEST P1 N1 P2 N2
The following output is generated.
Binomial Test for Equal Proportions
(Large Sample Case)
H0: P1 = P2
Ha: P1 <> P2
Sample 1:
Number of Observations: 38
Probability of Successes: 0.84210
Sample 2:
Number of Observations: 44
Probability of Successes: 0.88636
Pooled Probability of Success: 0.86585
Pooled Standard Deviation: 0.07547
Test Statistic: -0.58640
P-Value: 0.55760
CDF of Test Statistic: 0.27880
------------------------------------------------------------------------------
Null Hypothesis Null
Null Confidence Critical Acceptance Hypothesis
Hypothesis Level Value (+/-) Interval Conclusion
------------------------------------------------------------------------------
P1 = P2 50.0% 0.67 (0.250,0.750) ACCEPT
P1 = P2 80.0% 1.28 (0.100,0.900) ACCEPT
P1 = P2 90.0% 1.64 (0.050,0.950) ACCEPT
P1 = P2 95.0% 1.95 (0.025,0.975) ACCEPT
P1 = P2 97.5% 2.24 (0.0125,0.9875) ACCEPT
P1 = P2 99.0% 2.57 (0.005,0.995) ACCEPT
Date created: 01/23/2009 |
Last updated: 12/11/2023 Please email comments on this WWW page to alan.heckert@nist.gov. | ||||||||||||||||||||||