BLAND ALTMAN PLOT

BLAND ALTMAN PLOT

Graphics Command

Generates a Bland Altman plot for a paired set of measurements.

Given a set of paired measurements, X_i and Y_i for i = 1 to n, the Bland Altman plots the following

Vertical axis:	\( Y_{i} - X_{i} \)
Horizontal axis:	\( \frac{Y_{i} + X_{i}} {2} \)

That is, it plots the difference of the variables against their means. Often Y and X will represent two different measurement methods.

The Bland Altman plot is similar to the Tukey mean difference plot, but there are a few differences.

1. The Bland Altman plots are based on the raw data while the Tukey mean difference is based on plotting quantiles of the data.

2. The Bland Altman plot assumes the data are paired while the Tukey mean difference plot can be applied to either paired or unpaired data. Since the Tukey mean difference plots quantiles of the data sets, it does not require that the response variables to have the same length.

3. The Tukey mean difference plot is primarily focused on the question: do these two response variables have the same underlying distribution? The Bland Altman is primarily focused on the differences between the pairs (e.g., is there a systematic bias, is one method better than another, and so on).

Several reference lines are added to the Bland Altman plot (these can be omitted from plot with appropriate settings for the LINE and CHARACTER commands). Specifically, the following curves are generated

1	-	\( Y_{i} - X_{i} \) versus \( \frac{Y_{i} + X_{i}} {2} \)
2	-	a reference line at Y = 0 (this line denotes where the two samples are equal.
3	-	the mean of the \( Y_{i} - X_{i} \) points. This denotes the bias between the two samples.
4	-	\( \bar{Y} - \frac{\mbox{tppf}_{(0.975,n-1)}s} {\sqrt{n}} \) where \( \bar{Y} \) and s denote the mean and standard deviations of the differences ( \( Y_{i} - X_{i} \) ) repsectively, n denotes the sample size, and tppf is the percent point function of the t distribution. This is the lower confidence limit of the mean of the differences for normally distributed data.
5	-	\( \bar{Y} + \frac{\mbox{tppf}_{(0.975,n-1)}s} {\sqrt{n}} \). This is the upper confidence limit of the mean of the differences for normally distributed data.
6	-	\( \bar{Y} + 2 s \). This is the upper limit of agreement (if the differences are normally distributed, approximately 95% of the differences should lie within ± two standard deviations of the mean of the differences.
7	-	\( (\bar{Y} + 2 s) - \mbox{tppf}_{(0.975,n-1)} s \sqrt{\frac{3}{n}} \). This is an approximate 95% lower confidence limit for the upper limit of agreement.
8	-	\( (\bar{Y} + 2 s) + \mbox{tppf}_{(0.975,n-1)} s \sqrt{\frac{3}{n}} \). This is an approximate 95% upper confidence limit for the upper limit of agreement.
9	-	\( \bar{Y} - 2 s \). This the lower limit of agreement.
10	-	\( (\bar{Y} - 2 s) - \mbox{tppf}_{(0.975,n-1)} s \sqrt{\frac{3}{n}} \). This is an approximate 95% lower confidence limit for the lower limit of agreement.
11	-	\( (\bar{Y} - 2 s) + \mbox{tppf}_{(0.975,n-1)} s \sqrt{\frac{3}{n}} \). This is an approximate 95% upper confidence limit for the lower limit of agreement.

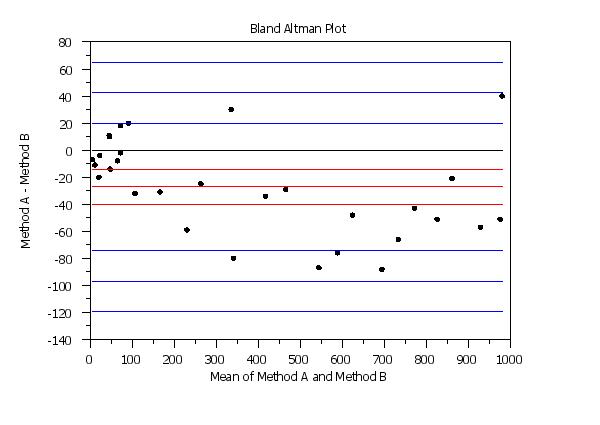
The reference line for the mean of the differences gives an indication of the bias between the two methods. If the bias is relatively consistent across the horizontal axis, the methods may be calibrated by simply subtracting (or adding) this value. If there is a trend as the mean values increase, then a linear, quadratic or some other more involved calibration may be required.

The limits of agreement can be used to asses whether the differences between the two methods are practically significant. If the differences are approximately normally distributed, then approximately 95% of the differences should be within these limits. If the limits of agreement are deemed clinically insignficant, then the two measurement methods may be considered equivalent for practical purposes. However, particularly for small samples, these limits of agreement may not be reliable. So the confidence limits for these can help give an indication of the uncertainty in these limits. These confidence limits are only approximate, but they should be adequate for most purposes.

The LINE and CHARACTER commands can be used to control the appearance of the plot. This is demonstrated in the Program examples below. Setting particular LINE or CHARACTER settings to BLANK can be used to omit some of the reference lines. Typically, the reference lines for the mean difference and the lower and upper limits of agreement will be included. However, you have control over all of them.

BLAND ALTMAN PLOT <y1> <y2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax assumes that the response variables contain the summary location statistic (typically the mean) for each group and that the groups are properly paired between the two response variables.

HIGHLIGHT BLAND ALTMAN PLOT <y1> <y2> <tag>
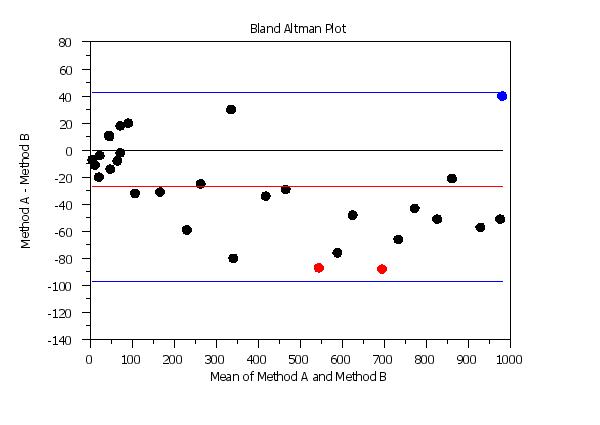
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <y2> is the second response variable;
            <tag> is a group-id variable that defines the highlighting;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax assumes that the response variables contain the summary location statistic (typically the mean) for each group and that the groups are properly paired between the two response variables. Both response variables and the highlight variable must have the same number of rows.

This syntax can be used to plot different plot points with different attributes. For example, it can be used to highlight groups in the data or to highlight points that indicate where the two methods are clinically different. It can also be used to label the plot points with the laboratory id.

You need to account for the number of groups in the variable when setting the LINE attributes. For example, if you have three groups, then the zero reference line is curve 4 rather than curve 2 (and all the other curves will be adjusted accordingly).

BLAND ALTMAN PLOT <y1> <x1> <y2> <x2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> is the first response variable;
            <x1> is the group-id variable corresponding to the first response variable;
            <y2> is the second response variable;
            <x2> is the group-id variable corresponding to the second response variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax is used for the case where you have raw data. The <y1> and <x1> variables should have the same number of elements and the <y2> and <x2> variables should have the same length. However, <y1> and <y2> are not required to have the same length.

Note that group-id variables should have the same group-id's. They do not need to be in the same order, but the distinct elements of <x1> and <x2> should be the same.

Highlighting (Syntax 2) is not supported for the raw data case.

BLAND ALTMAN PLOT Y1 Y2
BLAND ALTMAN PLOT Y1 Y2 SUBSET TAG > 2
HIGHLIGHT BLAND ALTMAN PLOT Y1 Y2 TAG

When the BLAND ALTMAN plot is generated, the following parameters are saved

DIFFMEAN	-	the mean of the differences (Y(i) - X(i))
DIFFSD	-	the standard deviation of the differences
DIFFMLCL	-	the lower 95% confidence limit for the mean of the differences
DIFFMUCL	-	the upper 95% confidence limit for the mean of the differences
LOWLIMIT	-	the lower limit of agreement
LOWLMLCL	-	the lower 95% confidence limit for the lower limit of agreement
LOWLMUCL	-	the upper 95% confidence limit for the lower limit of agreement
UPPLIMIT	-	the upper limit of agreement
UPPLMLCL	-	the lower 95% confidence limit for the upper limit of agreement
UPPLMUCL	-	the upper 95% confidence limit for the upper limit of agreement

These parameters can be used to label certain features of the plot.

It is sometimes preferred that percentage differences be plotted. That is, the vertical axis will plot
\( 100 \frac{Y_{i} - X_{i}} {(Y_{i} + X_{i})/2} \)

To plot percentage differences, enter

SET BLAND ALTMAN PLOT PERCENTAGES

To reset the default, enter

SET BLAND ALTMAN PLOT RAW

The following are written to the file dpst1f.dat using a 2E15.7 format

Column 1:	\( Y_{i} - X_{i} \)
Column 2:	\( \frac{Y_{i} + X_{i}} {2} \)

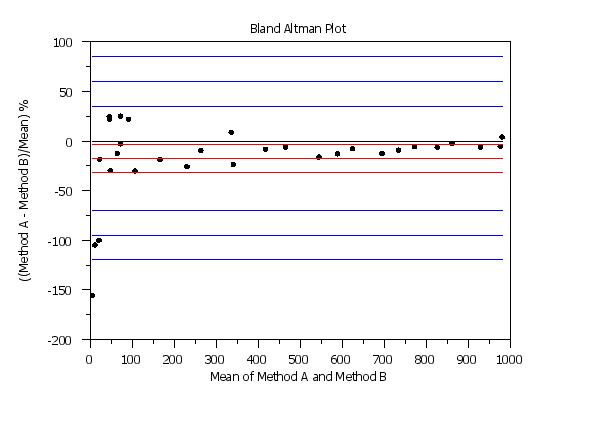
If percentage differences were requested, these will be written to column one rather than the raw differences.

This can be useful for the following purposes.

1. The various reference lines generated for the plot are based on the assumption that the differences are approximately normally distributed. You may want to generate a normal probability plot or perform some normal goodness of fit test for these differences.

2. If the differences seem to exhibit some trend as the average increases, then you may want to perform a fit to model this trend. This fit can be overlaid on the plot or used for calibration purposes.

For example, you can do something like the following

    SKIP 0
    READ dpst1f.dat YDIFF YAVE
    .
    NORMAL PROBABILITY PLOT YAVE
    NORMAL ANDERSON DARLING GOODNESS OF FIT YAVE
    .
    FIT YDIFF YAVE
    

For the raw data case, means will be computed for each distinct group. To request that medians be computed rather than means, enter
SET BLAND ALTMAN PLOT STATISTIC MEDIANS

To reset the default of means, enter

SET BLAND ALTMAN PLOT STATISTIC MEANS

The confidence intervals for the mean difference and for the lower and upper limits of agreement are based on the assumption that the differences are normally distributed. If this normality assumption is not satisfied, then you can request that they be generated using a bootstrap method. To request the bootstrap based confidence intervals, enter
SET BLAND ALTMAN PLOT CONFIDENCE INTERVALS BOOTSTRAP

To reset the default intervals, enter

SET BLAND ALTMAN PLOT CONFIDENCE INTERVALS ANALYTIC

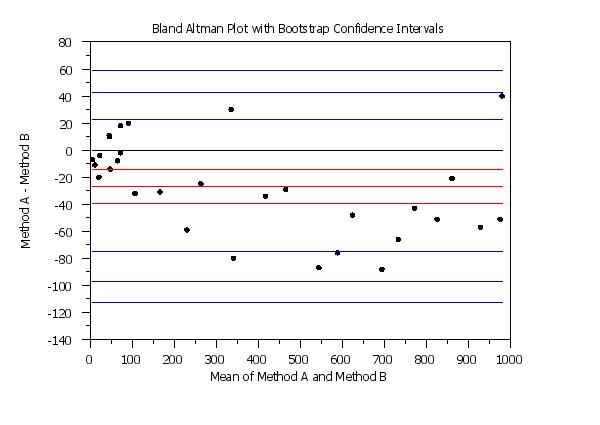
Note that it is the differences between the two sets of data that are bootstrapped, not the original response variables. It is recommended that you have at least 20 differences before using the bootstrap based confidence intervals.

The mean of the difference of the means, and the limit of agreement lines (\( \bar{Y} \pm 2s \) with \( \bar{Y} \) and s denoting the mean and standard deviation of the original differences) are computed as before. These 3 values are then computed for each bootstrap sample and the 2.5 and 97.5 percentiles of these bootstrap samples are used for the confidence limits.

None

BLAND ALTMAN HIGHLIGHT PLOT is a synonym for HIGHLIGHT BLAND ALTMAN PLOT

CHARACTERS	=	Sets the type for plot characters.
LINES	=	Sets the type for plot lines.
TUKEY MEAN DIFFERENCE PLOT	=	Generates a Tukey mean difference plot.
DIFFERENCE OF MEANS CONFIDENCE LIMITS	=	Generates a Tukey mean difference plot.
QUANTILE-QUANTILE PLOT	=	Generates a q-q plot.
BOX PLOT	=	Generates a box plot.
BIHISTOGRAM	=	Generates a bihistogram.
PLOT	=	Generates a data or function plot.
PROBABILITY PLOT	=	Generates a probability plot.
T-TEST	=	Carries out a 2-sample t test.
F-TEST	=	Carries out a 2-sample F test.

Giavarina (2015), "Understanding Bland Altman Analysis", Biochemia Medica, Vol. 25, No. 2, pp. 141-151.

Bland and Altman (1983), "Measurement in Medicine: The Analysis of Method Comparison Studies", Statistician, Vol. 32, pp. 307-317.

Exploratory Data Analysis

2017/07

 
. Step 1:   Read the data
.
skip 25
read bland.dat y1 y2
skip 0
.
. Step 2:   Set plot control features
.
case asis
title case asis
label case asis
title offset 2
y1label Method A - Method B
x1label Mean of Method A and Method B
title Bland Altman Plot
.
line blank solid solid dash dash solid dash dash solid dash dash
line color black black red red red blue blue blue blue blue blue
character circle
character hw 1.0 0.75
character fill on
.
ylimits -140 80
.
. Step 3:   Generate the plot
.
bland altman plot y1 y2
.
. Step 4:   Now generate the plot with uncertainty regions shaded
.
subregion on on on
let xmin = minimum xplot subset tagplot = 1
let xmax = maximum xplot subset tagplot = 1
subregion 1 xlimit xmin xmax
subregion 2 xlimit xmin xmax
subregion 3 xlimit xmin xmax
subregion 1 ylimit diffmlcl diffmucl
subregion 2 ylimit lowlmlcl lowlmucl
subregion 3 ylimit upplmlcl upplmucl
region fill on on on
region color g90 g90 g90
region border line bl bl bl
.
bland altman plot y1 y2
subregion off off off
region fill off off off
.
. Step 5:   Generate probability plot of the diffferences
.
skip 0
read dpst1f.dat ydiff
y1label Sorted Differences
x1label Percentils of Normal Distribution
Title Normal Probability Plot of Differences
ylimits
normal probability plot ydiff
    

 
. Step 1:   Read the data
.
skip 25
read bland.dat y1 y2
skip 0
.
. Step 2:   Set plot control features
.
case asis
title case asis
label case asis
title offset 2
y1label ((Method A - Method B)/Mean) %
x1label Mean of Method A and Method B
title Bland Altman Plot
.
line blank solid solid dash dash solid dash dash solid dash dash
line color black black red red red blue blue blue blue blue blue
character circle
character hw 1.0 0.75
character fill on
.
. Step 3:   Generate the plot
.
set bland altman plot percentage
bland altman plot y1 y2
    

 
. Step 1:   Read the data
.
skip 25
read bland.dat y1 y2
skip 0
let n = size y1
let tag = 1 for i = 1 1 n
let ydiff = y1 - y2
let tag = 2 subset ydiff < -80
let tag = 3 subset ydiff >  35
.
. Step 2:   Set plot control features
.
case asis
title case asis
label case asis
title offset 2
y1label Method A - Method B
x1label Mean of Method A and Method B
title Bland Altman Plot
.
line       blank blank blank solid solid blank blank solid blank blank ...
           solid blank blank
line color black black black black red   red   red   blue  blue  blue  ...
           blue  blue  blue
character circle circle circle
character hw 2.0 1.50 all
character fill on on on
character color black red blue
.
. Step 3:   Generate the plot
.
ylimits -140 80
highlight bland altman plot y1 y2 tag
    

 
. Step 1:   Read the data
.
skip 25
read bland.dat y1 y2
skip 0
.
. Step 2:   Set plot control features
.
case asis
title case asis
label case asis
title offset 2
y1label Method A - Method B
x1label Mean of Method A and Method B
title Bland Altman Plot with Bootstrap Confidence Intervals
.
line blank solid solid dash dash solid dash dash solid dash dash
line color black black red red red blue blue blue blue blue blue
character circle
character hw 1.0 0.75
character fill on
.
ylimits -140 80
.
. Step 3:   Generate the plot
.
bootstrap samples 10000
seed 31298
set random number generator fibbonacci congruential
set bland altman plot confidence intervals bootstrap
.
bland altman plot y1 y2