BOX COX NORMALITY PLOT

BOX-COX NORMALITY PLOT

Graphics Command

Generates a Box-Cox normality plot.

A Box-Cox normality plot is a graphical data analysis technique for determining the transformation (from the Box-Cox transformation family) that will yield a transformed variable that is "closest" to being normally distributed. The Box-Cox transformation family is essentially the power-transformation family (adjusted to include log transformations). The form for the family is:
\( T_{y} = \frac{y^{\lambda}}{\lambda} \)

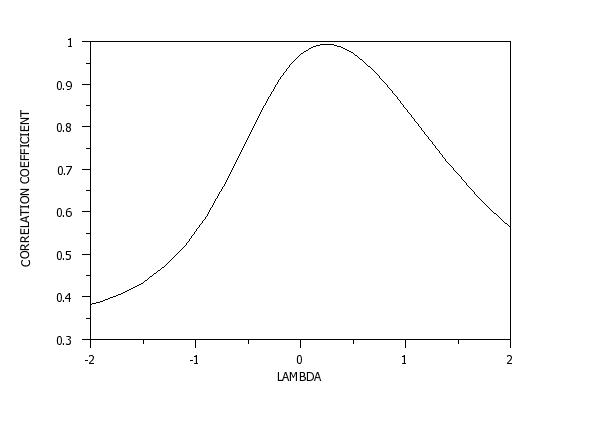
For each of selected members of the Box-Cox family, the transformation is carried out, a normal probability plot is computed, and the linearity of the normal probability plot is summarized via the correlation coefficient. The resulting normality plot thus consists of:

Vertical axis	=	normal probability plot correlation coefficient;
Horizontal axis	=	Box-Cox lambda parameter.

The value of the lambda parameter (on the horizontal axis) which corresponds to the maximum of the normal probability plot correlation coefficient curve (on the vertical axis) is of interest since it indicates the best-transformation member of the family. The normality technique is applicable for general transformation families. Currently, DATAPLOT only implements it for the Box-Cox family (the most important and common of the various transformation families).

BOX-COX NORMALITY PLOT <y>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is a response variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax generates a single Box-Cox normality plot. Note that <y> can also be a matrix argument. If <y> is a matrix, a single Box-Cox normality plot is generated for all the values in the matrix.

MULTIPLE BOX-COX NORMALITY PLOT <y1> ... <yk>
                        <SUBSET/EXCEPT/FOR qualification>
where <y1> ... <yk> is a list of response variables;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Note that response variables can also be matrices. If a matrix name is encountered, a Box-Cox normality plot will be drawn for all the values in the matrix.

REPLICATED BOX-COX NORMALITY PLOT <y> <x1>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is a response variable;
            <x1> is a group-id variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

A Box-Cox normality plot will be generated for each distinct value of the group-id variable. These plots will be overlaid on the same plot.

REPLICATED BOX-COX NORMALITY PLOT <y> <x1> <x2>
                        <SUBSET/EXCEPT/FOR qualification>
where <y> is a response variable;
            <x1> is a group-id variable;
            <x2> is a group-id variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The two group-id variables are cross-tabulated and a Box-Cox normality plot will be generated for each distinct combination of values for the group-id variables. These plots will be overlaid on the same plot.

BOX-COX NORMALITY PLOT Y
BOX-COX NORMALITY PLOT Y2
MULTIPLE BOX-COX NORMALITY PLOT Y1 TO Y5
REPLICATED BOX-COX NORMALITY PLOT Y X1

The TO syntax is supported for the BOX COX NORMALITY command. It is most useful for the MULTIPLE version of the command.

The following LET commands are also available:
LET A = BOX COX NORMALITY PPCC Y
LET A = BOX COX NORMALITY LAMBDA Y


These return the maximum PPCC value on the Box-Cox normality plot and the corresponding value of lambda, respectively.

These statistics can be used in a large number of plots and commands. For details, enter

HELP STATISTICS

None

BOX COX NORMALITY PLOT

BOX-COX LINE PLOT	= Generates a Box-Cox linearity plot.
BOX-COX HOMO PLOT	= Generates a Box-Cox homoscedasticity plot.
LET	= Transforms variables (and many other options).
PROBABILITY PLOT	= Generates a probability plot.
PPCC PLOT	= Generates a probability plot correlation coefficent plot.
PLOT	= Generates a data or function plot.

Box and Cox (1964), "An Analysis of of transformations," Journal of the Royal Statistical Society, Series B 26 (2): 211–252.

Exploratory Data Analysis

Pre-1987
2010/5: Support for MULTIPLE and REPLICATION options

 
LET Y = EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 100
Y1LABEL CORRELATION COEFFICIENT
X1LABEL LAMBDA
BOX-COX NORMALITY PLOT Y
    

 
title case asis
title offset 2
title automatic
label case asis
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
tic mark offset units screen
y1tic mark offset 2 0
.
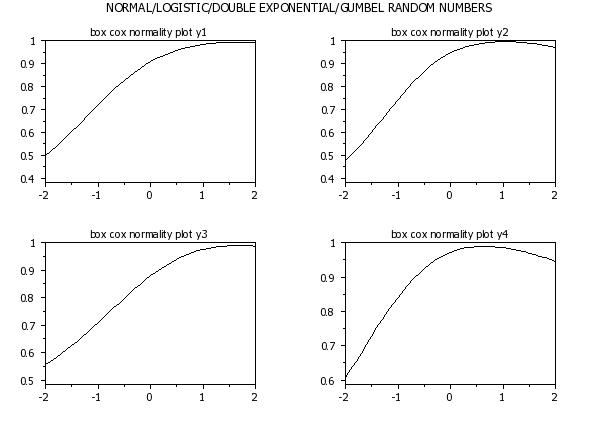
let y1 = norm rand numb for i = 1 1 100
let y2 = logistic rand numb for i = 1 1 100
let y3 = double exponential rand numb for i = 1 1 100
let y4 = gumbel rand numb for i = 1 1 100
multiplot 2 2
box cox normality plot y1
box cox normality plot y2
box cox normality plot y3
box cox normality plot y4
end of multiplot
move 50 97
just center
text Normal/Logistic/Double Exponential/Gumbel Random Numbers
.
line color blue red green cyan
multiple box cox normality plot y1 to y4
.
reset data
skip 25
read rehm.dat y1 y2 x1 x2
.
line color blue red green
replicated box cox normality plot y1 x2