GOODNESS OF FIT

GOODNESS OF FIT

Analysis Command

Perform Anderson-Darling, Kolmogorov-Smirnov, chi-square, or PPCC distributional goodness of fit tests.

There are a number of tests for assessing the goodness of fit for a distributional model. Several of these have been incorporated into this command. Specifically, the following goodness of fit methods are supported:
1. Kolmogorov-Smirnov
2. Anderson-Darling
3. Chi-Square
4. PPCC

Detailed descriptions of each of these methods is given below in the Notes section. As a general comment, goodness of fit methods are typically based on comparing the cumulative distribution of the data with a theoretical distribution or comparing the quantiles of the data with the a theoretical percent point function.

Previous versions of Dataplot supported separate commands (ANDERSON DARLING TEST, KOLMOGOROV SMIRNOV GOODNESS OF FIT TEST, and CHI-SQUARE GOODNESS OF FIT TEST). These separate commands have been replaced with the unified GOODNESS OF FIT command and are no longer available).

Some comments on this command.

1. Dataplot separates the estimation of distribution parameters from the goodness of fit assessment (the old version of the ANDERSON DARLING TEST would generate the maximum likelihood estimates if the user did not specify them).

   The location and scale parameters are specified generically with the following commands:

   LET KSLOC = <value>
   LET KSSCALE = <value>
   

   The location and scale parameters default to 0 and 1 if not specified.

   For distributions with one or more shape parameters, you should enter the values of the shape parameter.

   For a list of appropriate parameter values, enter

   HELP PROBABILITY DISTRIBUTIONS

2. For certain methods/distributions, appropriate critical values may be tabulated in published articles. Alternatively, critical values can be generated dynamically. See the Notes section below for each individual method for more information.

   Dynamically generated critical values are determined by generating 10,000 monte carlo simulations (and therefore computing 10,000 values of the goodness of fit statistic). The value of the goodness of fit statistic for the original data is compared to these monte carlo values to determine critical values and p-values.

   These dynamically generated critical values should be close to the published values, but they may not match exactly. This is due to the use of different random number generators and seed values. The differences tend to be greatest for small sample sizes.

   The advantage of using published tables is speed. The advantage of dynamically generated critical values is that a greater number of distributions are supported and there is more flexibility in specifying the alpha for the critical values (published tables are typically limited to a few values of ).

3. If critical values are determined dynamically, there are two distinct cases,
   • In the first case, we assume that the parameters are known.

   • In the second case, we assume that the parameters are not known (this is the more common case).

   This affects how the simulation is performed. In both cases, for a given simulation random numbers are generated using the specified parameters. For the case where the parameters are assumed known, the goodness of fit statistic is computed using the assumed known parameters. For the case where the parameters are assumed unknown, the parameters are estimated from the simulated random numbers first and then the goodness of fit statistic is computed using these fitted parameters.

   To specify which case is used, enter the command

   SET GOODNESS OF FIT FULLY SPECIFIED <ON/OFF>

   where ON means the parameters are assumed known and OFF means the parameters are assumed unknown.

   When the parameters must be estimated from the data, you can specify the fit method to use with the following command

   SET GOODNESS OF FIT FIT METHOD <ML/PPCC/DEFAULT>

   with ML and PPCC denoting maximum likelihood and PPCC methods, respectively. Using DEFAULT will select the fit method based on the goodness of fit criterion selected. For the DEFAULT choice, the Kolmogorov-Smirnov and Anderson-Darling goodness of fit criterion will use maximum likelihood and the PPCC goodness of fit criterion will use PPCC fitting. The chi-square method uses a chi-square approximation to obtain the critical values, so no simulation is required. The ML method will only be supported for distributions for which Dataplot supports maximum likelihood estimation.

   If maximum likelihood estimation is used, the following command can be used (see Note: section below for details)

   SET DISTRIBUTIONAL FIT TYPE <method>

<dist> <method> GOODNESS OF FIT <y>
                        <SUBSET/EXCEPT/FOR qualification>
where <dist> is one Dataplot's supported distributions;
            <method> is one of ANDERSON DARLING, KOLMOGOROV SMIRNOV, CHI-SQUARE, or PPCC;
            <y> is the response variable;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

Enter HELP PROBABILITY DISTRIBUTIONS for a list of supported distributions and the name of any required parameters.

<dist> <method> MULTIPLE GOODNESS OF FIT <y1> ... <yk>
                        <SUBSET/EXCEPT/FOR qualification>
where <dist> is one Dataplot's supported distributions;             <method> is one of ANDERSON DARLING, KOLMOGOROV SMIRNOV, CHI-SQUARE, or PPCC;
            <y1> ... <yk> is a list of 1 to 30 response variables;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax will generate the goodness of fit statistic for each variable in the list.

Note that the syntax

<dist> <method> MULTIPLE GOODNESS OF FIT Y1 TO Y4

is supported. This is equivalent to

<dist> <method> MULTIPLE GOODNESS OF FIT Y1 Y2 Y3 Y4

<dist> <method> REPLICATED GOODNESS OF FIT <y> <x1> ... <xk>
                        <SUBSET/EXCEPT/FOR qualification>
where <dist> is one Dataplot's supported distributions;
            <method> is one of ANDERSON DARLING, KOLMOGOROV SMIRNOV, CHI-SQUARE, or PPCC;
            <y> is the response variable;
            <x1> ... <xk> is a list of 1 to 6 group-id variables;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax peforms a cross-tabulation of ... and performs a goodness of fit test for each unique combination of cross-tabulated values. For example, if X1 has 3 levels and X2 has 2 levels, there will be a total of 6 goodness of fit tests performed.

Note that the syntax

<dist> <method> REPLICATED GOODNESS OF FIT Y X1 TO X4
is supported. This is equivalent to
<dist> <method> REPLICATED GOODNESS OF FIT Y X1 X2 X3 X4

<dist> CHI-SQUARE GOODNESS OF FIT <y> <x>
                        <SUBSET/EXCEPT/FOR qualification>
where <dist> is one Dataplot's supported distributions;
            <y> is a variable of pre-computed frequencies;
            <x> is a variable containing the mid-points of the bins;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax is used for the case where you have binned data with equal size bins.

Currently, only the chi-square goodness of fit method is supported for grouped data (although this may change in future releases).

<dist> CHI-SQUARE GOODNESS OF FIT <y> <xlow> <xhigh>
                        <SUBSET/EXCEPT/FOR qualification>
where <dist> is one Dataplot's supported distributions;
            <y> is a variable of pre-computed frequencies;
            <xlow> is a variable containing the lower limits of the bins;
            <xhigh> is a variable containing the upper limits of the bins;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax is used for the case where you have binned data with unequal size bins.

Currently, only the chi-square goodness of fit method is supported for grouped data (although this may change in future releases).

LET GAMMA = 2.5
LET KSLOC = 5
LET KSSCALE = 10
WEIBULL ANDERSON DARLING GOODNESS OF FIT Y
WEIBULL KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
WEIBULL PPCC GOODNESS OF FIT Y
WEIBULL CHI-SQUARE GOODNESS OF FIT Y

The Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N data points Y₁ Y₂ ..., Y_n the ECDF is defined as
\( E_{N} = n(i)/N \)

where n_i is the number of points less than Y_i This is a step function that increases by 1/N at the value of each data point.

The Kolmogorov-Smirnov goodness of fit test statistic is defined as

\( D = \max_{1 \le i \le N}|F(Y_{i}) - \frac{i} {N}| \)

where F is the theoretical cumulative distribution of the distribution being tested.

We can graph a plot of the empirical distribution function with a cumulative distribution function for a given distribution. The K-S test is based on the maximum distance between these two curves. An example of this plot for a sample of 100 normal random numbers is given here.

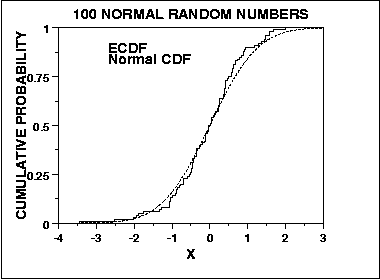
An attractive feature of this test is that the distribution of the K-S test statistic itself does not depend on the underlying cumulative distribution function being tested. Another advantage is that it is an exact test (the chi-square goodness of fit depends on an adequate sample size for the approximations to be valid). Despite these advantages, the K-S test has several important limitations:

1. It only applies to continuous distributions (there are extensions for discrete distributions, although these are not yet implemented in Dataplot).

2. The K-S test looks for the maximum difference wherever it occurs. That is, it is equally sensitive to differences at the centers and tails of the distribution. Some analysts prefer the Anderson-Darling test since it is designed to be more sensitive in the tails of the distribution.

3. The attractive feature that the critical values do not depend on the underlying distribution only applies if the distribution is fully specified (i.e., the parameters are assumed known).

   If the SET GOODNESS OF FIT FULLY SPECIFIED OFF command is entered, the K-S test will generate the critical values dynamically.

   For the fully specified case, you can specify whether to use published critical values (limited to a few specific values of alpha) or determine a more complete distribution via simulation with the command

   SET KOLMOGOROV SMIRNOV CRITICAL VALUES
             <TABLE/SIMULATION>

   There are several formulations for obtaining the tabled critical values in the literature. Dataplot uses the critical values from Chakravart, Laha, and Roy (see Reference: below).

The Anderson-Darling test (Stephens, 1974) is used to test if a sample of data comes from a specific distribution. It is a modification of the Kolmogorov-Smirnov (K-S) test and gives more weight to the tails than the K-S test. The K-S test is distribution free in the sense that the critical values do not depend on the specific distribution being tested. The Anderson-Darling test makes use of the specific distribution in calculating critical values. This has the advantage of allowing a more sensitive test and the disadvantage that critical values must be calculated for each distribution. For cases where published tables are not available, critical values can be computed dynamically via simulation. This extends the number of distributions for which the Anderson-Darling test can be used.

To specify whether published tables or simulation will be used to generate the critical values, enter the command (if the specified distribution does not support published tables, simulation will automatically be used).

SET ANDERSON DARLING CRITICAL VALUES           <TABLE/SIMULATION>

Currently, Dataplot supports critical values from published tables for the following distributions:

1. normal
2. lognormal
3. exponential
4. Weibull
5. extreme value type 1 (Gumbel)
6. logistic
7. double exponential
8. uniform ((0,1)
9. generalized pareto
10. Cauchy
11. Extreme Value Type 2 (Frechet)

Dynamic simulation of critical values for other distributions is available when there is a built-in maximum likelihood estimation procedure available (see the Note section below for the SET DISTRIBUTIONAL FIT TYPE command for a complete list of supported distributions).

Note that the uniform (0,1) case can be used for fully specified distributions (i.e., the shape, location, and scale parameters are not estimated from the data). Simply apply the appropriate CDF function to the data (this transforms it to a (0,1) interval) and apply the uniform (0,1) test to the transformed data.

The Anderson-Darling test statistic is

\( A^{2} = -N - S \)

where

\( S = \sum_{i=1}^{N}\frac{(2i - 1)}{N}[\log{F(Y_{i})} + \log{(1 - F(Y_{N+1-i}))}] \)

where F is the cumulative distribution function of interest.

The basic idea behind the chi-square goodness of fit test is to divide the range of the data into a number of intervals. Then the number of points that fall into each interval is compared to expected number of points for that interval if the data in fact come from the hypothesized distribution. More formally, the chi-square goodness of fit test statistic can be defined as follows.

For the chi-square goodness of fit, the data is divided into k bins and the test statistic is defined as

\( \chi^{2} = \sum_{i=1}^{k}(O_{i} - E_{i})^{2}/E_{i} \)

where O_i is the observed frequency for bin i and E_i is the expected frequency for bin i. The expected frequency is calculated by

\( E_{i} = F(Y_{u}) - F(Y_{l}) \)

where F is the cumulative distribution function for the distribution being tested, Y_u is the upper limit for class i, and Y_l is the lower limit for class i.

This test is sensitive to the choice of bins. There is no optimal choice for the bin width (since the optimal bin width depends on the distribution). Most reasonable choices should produce similar, but not identical, results.

This test is most frequently used when the data are received in pre-binned form (for raw data, the Anderson-Darling test is more powerful). However, you can use the chi-square test for raw data (you typically will want to have a reasonably large data set before doing this). For raw data, you can specify the binning with the commands CLASS WIDTH, CLASS LOWER, and CLASS UPPER. The default class width is 0.3 times the sample standard deviation. To specify other default algorithms, enter HELP HISTOGRAM CLASS WIDTH.

For the chi-square approximation to be valid, the expected frequency should be at least 5. The chi-square approximation may not be valid for small samples, and if some of the counts are less than five, you may need to combine some bins in the tails.

The test statistic follows, approximately, a chi-square distribution with (k - c) degrees of freedom where k is the number of non-empty cells and c = the number of parameters (including location and scale parameters and shape parameters) for the distribution + 1. For example, for a 3-parameter Weibull distribution, c = 4.

The primary advantage of the chi square goodnes of fit test is that it is quite general. It can be applied for any distribution, either discrete or continuous, for which the cumulative distribution function can be computed. Dataplot supports the chi-square goodness of fit test for all distributions for which it supports a CDF function.

There are several disadvantages:

1. The test is sensitive to how the binning of the data is performed.

2. It requires sufficient sample size so that the minimum expected frequency is five.

3. It is generally not as powerful as other goodness of fit tests such as the Anderson-Darling.

The PPCC method is supported for location/scale distributions and for distributions with a single shape parameter. Critical values are generated dynamically via simulation.

For more information on the PPCC method, enter HELP PPCC PLOT. Also see the NIST/SEMATACH e-Handbook of Statistical Methods:

http://www.itl.nist.gov/div898/handbook/eda/section3/ppccplot.htm

When the Anderson-Darling and Kolmogorov-Smirnov methods generate critical values dynamically, the maximum likelihood method is used to estimate the distribution parameters from the simulated data.

For several distributions, you can choose an alternative estimation method using the command

SET DISTRIBUTIONAL FIT TYPE <value>

where <value> can be one of the following (since this applies to the Anderson-Darling or Kolmogorov-Smirnov methods, only continuous distributions are listed).

ML (or MAXIMUM LIKELIHOOD):	use the default maximum likelihood, available for normal, uniform, logistic, double exponential, Cauchy, Gumbel, Slash, 1-para exponential, 2-para exponential, folded normal, 1-para Rayleigh, 2-para Rayleigh, 1-para Maxwell, 2-para Maxwell, 2-para Weibull, 3-para Weibull, 2-para inverted Weibull, 2-para lognormal, 2-para gamma, 2-para inverted gamma, 2-para geom extreme exponential, 2-para fatigue life, 2-para Frechet, 2-para Burr Type 10, 2-para logistic exponential, 2-para Von Mises (location/shape), triangular, Topp and Leone, power, reflected power, generalized Pareto, 2-para alpha, asymmetric Laplace, Pareto, truncated Pareto, 2-para brittle fiber Weibull, 2-para beta, 4-para beta, beta normal, two-sided power, reflected generalized Topp and Leone, normal mixture
BC (or BIAS CORRECTED):	use the bias corrected maximum likelihood, available for 1-para exponential, 2-para exponential, 2-para Weibull, 2-para inverted Weibull, 2-para Frechet
MOMENT:	use the moment estimates, available for uniform, Gumbel, 1-para Maxwell, 2-para Maxwell, 2-para gamma, 2-para inverted gamma, 2-para fatigue life, 2-para Beta, 4-para Beta, Pareto, generalized Pareto,
MODIFIED MOMENT:	use the modified moment estimates, available for the 3-para Weibull, 2-para Rayleigh, 3-para inverted Weibull, Pareto
LMOMENT (or L MOMEMNT):	use the L-moment estimates, available for generalized Pareto, generalized extreme value, Wakeby, Pearson Type 3, generalized logistic type 5, Kappa
PERCENTILE:	use Zynakis percentile method for the 3-para Weibull or 3-para inverted Weibull
WYCOFF BAIN ENGLEHARDT (or WBE):	use Wycoff, Bain, Englehardt percentile method for the 3-para Weibull or 3-para inverted Weibull
ELEMENTAL PERCENTILE:	use the elemental percentile method, available for the generalized Pareto, generalized extremed value
ORDER STATISTIC (or OS):	use the order statistic method, available for Cauchy
WEIGHTED ORDER STATISTIC (or WOS):	use the weighted order statistic method, available for Cauchy

Note that the above list gives the distributions for which dynamic critical values can be obtained by simulation when the parameters are assumed unknown for the Anderson-Darling and Kolmogorov-Smirnov methods. If a particular distribution only supports a single method (e.g., several currently only support L-moment estimates), that method will always be used. If you specify a method that is not supported for a given distribution, the default method (usually maximum likelihood) will be used.

Also note that a given estimation method for a particular distribution may fail for certain data sets. Since a large number of simulated data sets are generated, this may be an issue for some distributions. The output will return the number of times a failure in the estimation procedure was detected in the simulations.

None

GOODNESS OF FIT TEST is a synonym for GOODNESS OF FIT
GOF is a synonym for GOODNESS OF FIT

WILK SHAPIRO TEST	= Perform a Wilks-Shapiro test for normality.
MAXIMUM LIKELIHOOD	= Perform maximum likelihood estimation for several distributions.
PROBABILITY PLOT	= Generate a probability plot.
PPCC PLOT	= Generate a PPCC plot.
HISTOGRAM	= Generates a histogram.
RANDOM NUMBERS	= Generate random numbers.

Stephens, M. A. (1974), "EDF Statistics for Goodness of Fit and Some Comparisons," Journal of the American Statistical Association, Vol. 69, pp. 730-737.

Stephens, M. A. (1976), "Asymptotic Results for Goodness-of-Fit Statistics with Unknown Parameters," Annals of Statistics, Vol. 4, pp. 357-369.

Stephens, M. A. (1977), "Goodness of Fit for the Extreme Value Distribution," Biometrika, Vol. 64, pp. 583-588.

Stephens, M. A. (1977), "Goodness of Fit with Special Reference to Tests for Exponentiality," Technical Report No. 262, Department of Statistics, Stanford University, Stanford, CA.

Stephens, M. A. (1979), "Tests of Fit for the Logistic Distribution Based on the Empirical Distribution Function," Biometrika, Vol. 66, pp. 591-595.

"MIL-HDBK-17 Volume 1: Guidelines for Characterization of Structural Materials", Depeartment of Defense, chapter 8. The URL for MIL-HDBK-17 is http://mil-17.udel.edu/.

V. Choulakian and M. A. Stephens (2001), "Goodness-of-Fit Tests for the Generalized Pareto Distribution", Technometrics, Vol. 43, No. 4, pp. 478-484.

James J. Filliben (1975), "The Probability Plot Correlation Coefficient Test for Normality," Technometrics, Vol. 17, No. 1.

Chakravart, Laha, and Roy (1967), "Handbook of Methods of Applied Statistics, Volume I," John Wiley, pp. 392-394.

Snedecor and Cochran (1989), "Statistical Methods", Eight Edition, Iowa State, 1989, pp. 76-79.

Distributional Modeling

2009/10

.  Step 1: Read the data
.
.          Following data from Jeffery Fong of the NIST
.          Applied and Computational Mathematics Division.
.          This is strength data in ksi units.
.
read y
18.830
20.800
21.657
23.030
23.230
24.050
24.321
25.500
25.520
25.800
26.690
26.770
26.780
27.050
27.670
29.900
31.110
33.200
33.730
33.760
33.890
34.760
35.750
35.910
36.980
37.080
37.090
39.580
44.045
45.290
45.381
end of data
.
.  Step 2: Apply goodness of fit tests for Weibull distribution
.          based on ML estimates
.
set write decimals 5
3-parameter weibull mle y
let ksloc = locml
let ksscale = scaleml
let gamma = shapeml
.
.          Anderson-Darling
.
set anderson darling critical values table
weibull anderson darling goodness of fit y
set anderson darling critical values simulation
weibull anderson darling goodness of fit y
.
.  Step 3: Apply goodness of fit tests for normal distribution
.
normal mle y
let ksloc = xmean
let ksscale = xsd
.
set anderson darling critical values table
normal anderson darling goodness of fit y
set anderson darling critical values simulation
normal anderson darling goodness of fit y
set kolmogorov smirnov critical values simulation
normal kolmogorov smirnov goodness of fit y
    

The following output is generated.

      *********************************
      **  3-parameter weibull mle y  **
      *********************************
 
 
            Three-Parameter Weibull (Minimum) Parameter Estimation:
                               Full Sample Case
 
Summary Statistics:
Number of Observations:                              31
Sample Mean:                                   30.81141
Sample Standard Deviation:                      7.25338
Sample Skewness:                                0.39880
Sample Minimum:                                18.82999
Sample Maximum:                                45.38100
 
Zanakis Percentile Method:
Estimate of Location:                          18.65836
Estimate of Scale:                             15.10163
Estimate of Shape:                              1.86735
Value of Log-Likelihood Function:            -104.60286
AIC:                                          215.20572
AICC:                                         216.09461
BIC:                                          219.50768
 
Wycoff-Bain-Englehardt Percentile Method
Estimate of Location:                          16.64362
Estimate of Scale:                             16.41275
Estimate of Shape:                              1.92760
Value of Log-Likelihood Function:            -103.63967
AIC:                                          213.27934
AICC:                                         214.16823
BIC:                                          217.58131
 
Modified Moments:
Estimate of Location:                          15.60378
Estimate of Scale:                             17.17121
Estimate of Shape (Gamma):                      2.21477
Standard Error of Location:                     0.71154
Standard Error of Scale:                        0.52547
Standard Error of Shape:                        0.09924
Value of Log-Likelihood Function:            -103.56460
AIC:                                          213.12921
AICC:                                         214.01810
BIC:                                          217.43118
 
Maximum Likelihood:
Estimate of Location:                          17.64420
Estimate of Scale:                             14.83507
Estimate of Shape (Gamma):                      1.91358
Value of Log-Likelihood Function:            -103.26267
AIC:                                          212.52535
AICC:                                         213.41423
BIC:                                          216.82731
 
 
      *************************
      **  let ksloc = locml  **
      *************************
 
 
THE COMPUTED VALUE OF THE CONSTANT KSLOC    =   0.1764420E+02
 
 
      *****************************
      **  let ksscale = scaleml  **
      *****************************
 
 
THE COMPUTED VALUE OF THE CONSTANT KSSCALE  =   0.1483507E+02
 
 
      ***************************
      **  let gamma = shapeml  **
      ***************************
 
 
THE COMPUTED VALUE OF THE CONSTANT GAMMA    =   0.1913580E+01
 
      ***********************************
      **  .          Anderson-Darling  **
      ***********************************
 
      **************************************************
      **  set anderson darling critical values table  **
      **************************************************
 
 
THE FORTRAN COMMON CHARACTER VARIABLE ANDEDARL HAS JUST BEEN SET TO TABL
 
      **************************************************
      **  weibull anderson darling goodness of fit y  **
      **************************************************
 
 
            Anderson-Darling Goodness of Fit Test
            (Critical Values from Published Tables)
 
Response Variable: Y
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: WEIBULL
Location Parameter:                               17.64420
Scale Parameter:                                  14.83507
Shape Parameter 1:                                 1.91358
 
Summary Statistics:
Number of Observations:                                 31
Sample Minimum:                                   18.82999
Sample Maximum:                                   45.38100
Sample Mean:                                      30.81141
Sample SD:                                         7.25338
 
Anderson-Darling Test Statistic Value:             0.33805
Adjusted Test Statistic Value:                     0.35019
 
 
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%            0.637      Accept H0
     5%    95%            0.757      Accept H0
   2.5%  97.5%            0.877      Accept H0
     1%    99%            1.038      Accept H0
 
 
      *******************************************************
      **  set anderson darling critical values simulation  **
      *******************************************************
 
 
THE FORTRAN COMMON CHARACTER VARIABLE ANDEDARL HAS JUST BEEN SET TO SIMU
 
      **************************************************
      **  weibull anderson darling goodness of fit y  **
      **************************************************
 
 
            Anderson-Darling Goodness of Fit Test
                   (Fully Specified Model)
 
Response Variable: Y
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: WEIBULL
Location Parameter:                               17.64420
Scale Parameter:                                  14.83507
Shape Parameter 1:                                 1.91358
 
Summary Statistics:
Number of Observations:                                 31
Sample Minimum:                                   18.82999
Sample Maximum:                                   45.38100
Sample Mean:                                      30.81141
Sample SD:                                         7.25338
 
Anderson-Darling Test Statistic Value:             0.33805
Number of Monte Carlo Simulations:             10000.00000
CDF Value:                                         0.09370
P-Value                                            0.90630
 
 
 
Percent Points of the Reference Distribution
-----------------------------------
  Percent Point               Value
-----------------------------------
            0.0    =          0.000
           50.0    =          0.772
           75.0    =          1.248
           90.0    =          1.964
           95.0    =          2.579
           97.5    =          3.230
           99.0    =          4.115
           99.5    =          4.814
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%            1.964      Accept H0
     5%    95%            2.579      Accept H0
   2.5%  97.5%            3.230      Accept H0
     1%    99%            4.115      Accept H0
 
  *Critical Values Based on    10000 Monte Carlo Simulations



      ********************
      **  normal mle y  **
      ********************
 
 
            Normal Parameter Estimation
 
Summary Statistics:
Number of Observations:                              31
Sample Minimum:                                18.82999
Sample Maximum:                                45.38100
 
 
Maximum Likelihood:
Estimate of Location (Mean):                   30.81141
Standard Error of Location:                     1.30274
Estimate of Scale (SD):                         7.25338
Standard Error of Scale:                        0.93640
Log-likelihood:                          -0.1049126E+03
AIC:                                      0.2138252E+03
AICc:                                     0.2142538E+03
BIC:                                      0.2166932E+03
 
 
Confidence Interval for Location Parameter (Normal Approximation)
---------------------------------------------
     Confidence          Lower          Upper
    Coefficient          Limit          Limit
---------------------------------------------
          50.00       29.92196       31.70087
          75.00       29.28321       32.33962
          90.00       28.60032       33.02251
          95.00       28.15085       33.47198
          99.00       27.22887       34.39396
          99.90       26.06166       35.56117
---------------------------------------------
 
 
Confidence Interval for Scale Parameter (Normal Approximation)
---------------------------------------------
     Confidence          Lower          Upper
    Coefficient          Limit          Limit
---------------------------------------------
          50.00        6.73462        8.03002
          75.00        6.35897        8.58825
          90.00        6.00479        9.23849
          95.00        5.79626        9.69540
          99.00        5.42284       10.69967
          99.90        5.03893       12.08652
---------------------------------------------
 
 
      *************************
      **  let ksloc = xmean  **
      *************************
 
 
THE COMPUTED VALUE OF THE CONSTANT KSLOC    =   0.3081142E+02
 
 
      *************************
      **  let ksscale = xsd  **
      *************************
 
 
THE COMPUTED VALUE OF THE CONSTANT KSSCALE  =   0.7253381E+01
 
 
      **************************************************
      **  set anderson darling critical values table  **
      **************************************************
 
 
THE FORTRAN COMMON CHARACTER VARIABLE ANDEDARL HAS JUST BEEN SET TO TABL
 
      *************************************************
      **  normal anderson darling goodness of fit y  **
      *************************************************
 
 
            Anderson-Darling Goodness of Fit Test
            (Critical Values from Published Tables)
 
Response Variable: Y
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: NORMAL
Location Parameter:                               30.81141
Scale Parameter:                                   7.25338
 
Summary Statistics:
Number of Observations:                                 31
Sample Minimum:                                   18.82999
Sample Maximum:                                   45.38100
Sample Mean:                                      30.81141
Sample SD:                                         7.25338
 
Anderson-Darling Test Statistic Value:             0.53219
Adjusted Test Statistic Value:                     0.58701
 
 
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%            0.616      Accept H0
     5%    95%            0.735      Accept H0
   2.5%  97.5%            0.861      Accept H0
     1%    99%            1.020      Accept H0
 
 
      *******************************************************
      **  set anderson darling critical values simulation  **
      *******************************************************
 
 
THE FORTRAN COMMON CHARACTER VARIABLE ANDEDARL HAS JUST BEEN SET TO SIMU
 
      *************************************************
      **  normal anderson darling goodness of fit y  **
      *************************************************
 
 
            Anderson-Darling Goodness of Fit Test
                   (Fully Specified Model)
 
Response Variable: Y
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: NORMAL
Location Parameter:                               30.81141
Scale Parameter:                                   7.25338
 
Summary Statistics:
Number of Observations:                                 31
Sample Minimum:                                   18.82999
Sample Maximum:                                   45.38100
Sample Mean:                                      30.81141
Sample SD:                                         7.25338
 
Anderson-Darling Test Statistic Value:             0.53219
Number of Monte Carlo Simulations:             10000.00000
CDF Value:                                         0.29750
P-Value                                            0.70250
 
 
 
Percent Points of the Reference Distribution
-----------------------------------
  Percent Point               Value
-----------------------------------
            0.0    =          0.000
           50.0    =          0.764
           75.0    =          1.231
           90.0    =          1.919
           95.0    =          2.478
           97.5    =          3.115
           99.0    =          3.942
           99.5    =          4.535
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%            1.919      Accept H0
     5%    95%            2.478      Accept H0
   2.5%  97.5%            3.115      Accept H0
     1%    99%            3.942      Accept H0
 
  *Critical Values Based on    10000 Monte Carlo Simulations
 
      *********************************************************
      **  set kolmogorov smirnov critical values simulation  **
      *********************************************************
 
 
THE FORTRAN COMMON CHARACTER VARIABLE KOLMSMIR HAS JUST BEEN SET TO SIMU
 
      ***************************************************
      **  normal kolmogorov smirnov goodness of fit y  **
      ***************************************************
 
 
            Kolmogorov-Smirnov Goodness of Fit Test
 
Response Variable: Y
 
H0: The distribution fits the data
Ha: The distribution does not fit the data
 
Distribution: NORMAL
Location Parameter:                               30.81141
Scale Parameter:                                   7.25338
 
Summary Statistics:
Number of Observations:                                 31
Sample Minimum:                                   18.82999
Sample Maximum:                                   45.38100
Sample Mean:                                      30.81141
Sample SD:                                         7.25338
 
Kolmogorov-Smirnov Test Statistic Value:           0.15139
Number of Monte Carlo Simulations:             10000.00000
CDF Value:                                         0.57660
P-Value                                            0.42340
 
 
 
            (Fully Specified Model)
 
Percent Points of the Reference Distribution
-----------------------------------
  Percent Point               Value
-----------------------------------
            0.0    =          0.000
           50.0    =          0.143
           75.0    =          0.176
           90.0    =          0.213
           95.0    =          0.236
           97.5    =          0.256
           99.0    =          0.284
           99.5    =          0.305
 
Conclusions (Upper 1-Tailed Test)
----------------------------------------------
  Alpha    CDF   Critical Value     Conclusion
----------------------------------------------
    10%    90%            0.213      Accept H0
     5%    95%            0.236      Accept H0
     1%    99%            0.284      Accept H0
 
  *Critical Values Based on    10000 Monte Carlo Simulations