SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 1 Vol 2

TRIMMED MEAN CONFIDENCE LIMITS

Name:
    TRIMMED MEAN CONFIDENCE LIMITS
Type:
    Analysis Command
Purpose:
    Generates a trimmed mean based confidence interval for the location of a variable.
Description:
    Mosteller and Tukey (see Reference section below) define two types of robustness:

    1. resistance means that changing a small part, even by a large amount, of the data does not cause a large change in the estimate

    2. robustness of efficiency means that the statistic has high efficiency in a variety of situations rather than in any one situation. Efficiency means that the estimate is close to optimal estimate given that we distribution that the data comes from. A useful measure of efficiency is:

        Efficiency = (lowest variance feasible)/(actual variance)

    Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency.

    Standard confidence intervals are based on the mean and variance. These are the optimal estimators if the data are in fact from a Gaussian population. However, they lack both resistance and robustness of efficiency. The trimmed mean is computed by removing a specified percentage of data values in each tail. The trimmed mean is less affected by outliers (i.e., resistance) than the mean. On the other hand, it uses more information than the median (i.e., robustness of efficiency) than the median. That is, the trimmed mean provides a location measure that is more resistant than the mean, but has more robustness of efficiency than the median.

    The trimmed mean confidence interval for the population trimmed mean location is defined by:

      xbar(t) +/- TPPF(1-alpha/2,n-g-1)*s(w)/[(1-lambda)*SQRT(n)]

    where

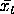      xbar(t) = sample trimmed mean
      t = the t percent point function
      sw = the sample Winsorized standard deviation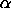
      alpha = the significance level
      n = the sample size
      p1 = fraction trimmed from lower tail
      p2 = fraction trimmed from upper tail
      g = integer portion of n(p1 + p2)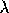
      lambda = p1 + p2
Syntax:
    TRIMMED MEAN CONFIDENCE LIMITS <y>       <SUBSET/EXCEPT/FOR qualification>
    where <y> is the response variable,
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET P1 = 10
    LET P2 = 10
    TRIMMED MEAN CONFIDENCE LIMITS Y1

    LET P1 = 20
    LET P2 = 20
    TRIMMED MEAN CONFIDENCE LIMITS Y1 SUBSET TAG > 2

Note:
    The trimming percentages are specified with the LET command. Specifically, define the parameters P1 (lower trimming percentage) and P2 (upper trimming percentage). For example,

      LET P1 = 10 LET P2 = 10
Note:
    A table of confidence intervals is printed for alpha levels of 50.0, 75.0, 90.0, 95.0, 99.0, 99.9, 99.99, and 99.999. The sample trimmed mean estimate and sample trimmed mean standard error are also printed. The t-value and t-value X standard error are printed in the table.
Note:
    You can also compute a confidence interval using the TRIMMED MEAN BOOTSTRAP PLOT. Wilcox recommends using the "percentile t bootstrap" method (this is a refinement of the trimmed mean bootstrap estimate). The "percentile t bootstrap" is not currently supported in Dataplot.
Default:
    None
Synonyms:
    TRIMMED MEAN CONFIDENCE INTERVAL
Related Commands:
    CONFIDENCE LIMITS = Compute a Gaussian based confidence limit.
    BIWEIGHT CONFIDENCE LIMITS = Compute a trimmed mean based confidence limit.
    T-TEST = Perform a t-test.
    TRIMMED MEAN PLOT = Generate a trimmed mean (versus subset plot).
    TRIMMED MEAN = Compute a trimmed mean.
    WINSORIZED MEAN = Compute a Winsorized mean.
Reference:
    "Introduction to Robust Estimation and Hypothesis Testing", Rand R. Wilcox, Academic Press, 1997.
Applications:
    Robust Data Analysis
Implementation Date:
    2003/2
Program: 
     
LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 100
LET Y2 = LOGISTIC RANDOM NUMBERS FOR I = 1 1 100
LET Y3 = CAUCHY RANDOM NUMBERS FOR I = 1 1 100
LET Y4 = DOUBLE EXPONENTIAL RANDOM NUMBERS FOR I = 1 1 100
LET P1 = 10
LET P2 = 10
TRIMMED MEAN CONFIDENCE LIMITS Y1
TRIMMED MEAN CONFIDENCE LIMITS Y2
TRIMMED MEAN CONFIDENCE LIMITS Y3
TRIMMED MEAN CONFIDENCE LIMITS Y4
    Dataplot generates the following output: 
     
  
       *****************************************
       **  TRIMMED MEAN CONFIDENCE LIMITS Y1  **
       *****************************************
  
  
                    CONFIDENCE LIMITS FOR TRIMMED MEAN LOCATION
                            (2-SIDED)
  
           NUMBER OF OBSERVATIONS         =      100
           PERCENTAGE TRIMMED BELOW       =    10.00000
           PERCENTAGE TRIMMED ABOVE       =    10.00000
           TRIMMED MEAN LOCATION          =  -0.1999552E-01
           TRIMMED MEAN STANDARD ERROR    =   0.8344749E-01
           DEGREES OF FREEDOM             =       79
  
    CONFIDENCE   T     T X STDERR       LOWER         UPPER
    VALUE (%)  VALUE                    LIMIT         LIMIT
 ---------------------------------------------------------------
      50.000   0.678  0.565447E-01  -.765402E-01  0.365492E-01
      75.000   1.159  0.967048E-01  -.116700      0.767093E-01
      90.000   1.664  0.138888      -.158883      0.118892
      95.000   1.990  0.166098      -.186094      0.146103
      99.000   2.640  0.220260      -.240256      0.200265
      99.900   3.418  0.285224      -.305220      0.265229
      99.990   4.099  0.342015      -.362011      0.322020
      99.999   4.721  0.393923      -.413919      0.373928
  
  
       *****************************************
       **  TRIMMED MEAN CONFIDENCE LIMITS Y2  **
       *****************************************
  
  
                    CONFIDENCE LIMITS FOR TRIMMED MEAN LOCATION
                            (2-SIDED)
  
           NUMBER OF OBSERVATIONS         =      100
           PERCENTAGE TRIMMED BELOW       =    10.00000
           PERCENTAGE TRIMMED ABOVE       =    10.00000
           TRIMMED MEAN LOCATION          =   0.8123081E-01
           TRIMMED MEAN STANDARD ERROR    =   0.1910256
           DEGREES OF FREEDOM             =       79
  
    CONFIDENCE   T     T X STDERR       LOWER         UPPER
    VALUE (%)  VALUE                    LIMIT         LIMIT
 ---------------------------------------------------------------
      50.000   0.678  0.129440      -.482097E-01  0.210671
      75.000   1.159  0.221374      -.140143      0.302605
      90.000   1.664  0.317938      -.236707      0.399168
      95.000   1.990  0.380227      -.298996      0.461458
      99.000   2.640  0.504213      -.422982      0.585444
      99.900   3.418  0.652927      -.571696      0.734158
      99.990   4.099  0.782931      -.701701      0.864162
      99.999   4.721  0.901758      -.820527      0.982989
  
  
       *****************************************
       **  TRIMMED MEAN CONFIDENCE LIMITS Y3  **
       *****************************************
  
  
                    CONFIDENCE LIMITS FOR TRIMMED MEAN LOCATION
                            (2-SIDED)
  
           NUMBER OF OBSERVATIONS         =      100
           PERCENTAGE TRIMMED BELOW       =    10.00000
           PERCENTAGE TRIMMED ABOVE       =    10.00000
           TRIMMED MEAN LOCATION          =   0.2256883
           TRIMMED MEAN STANDARD ERROR    =   0.1878559
           DEGREES OF FREEDOM             =       79
  
    CONFIDENCE   T     T X STDERR       LOWER         UPPER
    VALUE (%)  VALUE                    LIMIT         LIMIT
 ---------------------------------------------------------------
      50.000   0.678  0.127293      0.983956E-01  0.352981
      75.000   1.159  0.217701      0.798762E-02  0.443389
      90.000   1.664  0.312662      -.869737E-01  0.538350
      95.000   1.990  0.373918      -.148230      0.599606
      99.000   2.640  0.495847      -.270158      0.721535
      99.900   3.418  0.642093      -.416405      0.867781
      99.990   4.099  0.769940      -.544252      0.995628
      99.999   4.721  0.886795      -.661106       1.11248
  
  
       *****************************************
       **  TRIMMED MEAN CONFIDENCE LIMITS Y4  **
       *****************************************
  
  
                    CONFIDENCE LIMITS FOR TRIMMED MEAN LOCATION
                            (2-SIDED)
  
           NUMBER OF OBSERVATIONS         =      100
           PERCENTAGE TRIMMED BELOW       =    10.00000
           PERCENTAGE TRIMMED ABOVE       =    10.00000
           TRIMMED MEAN LOCATION          =  -0.1246601E-01
           TRIMMED MEAN STANDARD ERROR    =   0.9687326E-01
           DEGREES OF FREEDOM             =       79
  
    CONFIDENCE   T     T X STDERR       LOWER         UPPER
    VALUE (%)  VALUE                    LIMIT         LIMIT
 ---------------------------------------------------------------
      50.000   0.678  0.656421E-01  -.781081E-01  0.531761E-01
      75.000   1.159  0.112264      -.124730      0.997976E-01
      90.000   1.664  0.161233      -.173699      0.148767
      95.000   1.990  0.192821      -.205287      0.180355
      99.000   2.640  0.255697      -.268163      0.243231
      99.900   3.418  0.331114      -.343580      0.318648
      99.990   4.099  0.397042      -.409508      0.384576
      99.999   4.721  0.457301      -.469767      0.444835
Date created: 02/25/2003
Last updated: 12/11/2023
Please email comments on this WWW page to alan.heckert@nist.gov.