Dataplot

Vol 2

Vol 1

BER

BER (LET)

Library Function

Compute the ber Kelvin function or the derivative of the ber Kelvin function.

The ber Kelvin function can then be defined in terms of the Bessel function of the first kind:

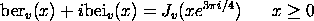
where J_v is the Bessel function of the first kind.

The functions described here compute these functions for the case when there is a real, non-negative input argument and order zero (i.e., v = 0).

Dataplot computes these function using the KLVNA routines from "Computation of Special Functions" (see the References section below).

LET <yr> = BER(<x>) <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative number, variable or parameter;
          <yr> is a variable or a parameter (depending on what <x> is) where the computed Kelvin value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the real component of the Kelvin function of the first kind.

LET <yc> = BERI(<x>) <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative number, variable or parameter;
          <yc> is a variable or a parameter (depending on what <x> is) where the computed Kelvin value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the complex component of the Kelvin function of the first kind.

LET <yr> = BER1(<x>) <SUBSET/EXCEPT/FOR qualification> where <x> is a non-negative number, variable or parameter;
          <yr> is a variable or a parameter (depending on what <x> is) where the computed Kelvin value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the real component of the derivative of the Kelvin function of the first kind.

LET <yc> = BERI1(<x>) <SUBSET/EXCEPT/FOR qualification>
where <x> is a non-negative number, variable or parameter;
          <yc> is a variable or a parameter (depending on what <x> is) where the computed Kelvin value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

This syntax computes the complex component of the derivative of the Kelvin function of the first kind.

LET A = BER(2)
LET A = BERI(2)
LET A = BER1(2)
LET A = BERI1(2)


LET YR = BER(X)
LET YC = BERI(X)

Library functions are distinguished from let subcommands in the following ways.
1. Functions enclose the input value in parenthesis. Let subcommands use spaces.

2. Functions can accept (and return) either parameters (i.e., single values) or variables (i.e., an array of values) while let subcommands are specific in which they accept as input and what they return as output.

3. Functions can accept expressions while let subcommands do not. For example, the following is legal:
   LET Y2 = ABS(Y1-INT(Y1))

   For let subcommands, you typically have to do something like the following:

   LET YTEMP = Y**2 + 8
   LET A = SUM YTEMP
   

None

None

KER	= Compute the Ker Kelvin functions.
CBESSJ	= Compute the Bessel function of the first kind with complex argument.
CBESSY	= Compute the Bessel function of the second kind with complex argument.
CBESSI	= Compute the modified Bessel function with complex argument.
CBESSK	= Compute the modified Bessel function of the third kind with complex argument.
BESSKN	= Compute the Bessel function of the third kind with real argument.
BESSIN	= Compute the modified Bessel function with real argument.
BESSJN	= Compute the Bessel function of the first kind with real argument.

"Computation of Special Functions", Shanjie Zhang and Jianming Jin, John Wiley and Sons, 1996, chapter 9.

"Handbook of Mathematical Functions, Applied Mathematics Series, Vol. 55", Abramowitz and Stegun, National Bureau of Standards, 1964 (pages 379-385).

Special Functions

1997/12

LINE SOLID DASH
TITLE BER KELVIN FUNCTION
PLOT BER(X) FOR X = 0.1 0.1 10 AND
PLOT BERI(X) FOR X = 0.1 0.1 10