

|
BGEPDFName:
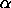 and and
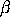 . .
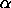 and
and 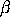 ,
the resulting distribution is referred to as a beta-geometric
distribution. For a standard geometric distribution, p
is assumed to be fixed for successive trials. For the
beta-geometric distribution, the value of p changes
for each trial. ,
the resulting distribution is referred to as a beta-geometric
distribution. For a standard geometric distribution, p
is assumed to be fixed for successive trials. For the
beta-geometric distribution, the value of p changes
for each trial.
The beta-geometric distribution has the following probability density function:
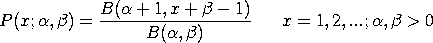
with
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing non-negative integer values; <alpha> is a number, parameter, or variable that specifies the first shape parameter; <beta> is a number, parameter, or variable that specifies the second shape parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed beta-geometric pdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET A = BGEPDF(X,2.1,4) PLOT BGEPDF(X,ALPHA,BETA) FOR X = 1 1 20
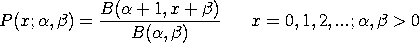
We will refer to the first parameterization as the unshifted parameterization and the second parameterization as the shifted parameterization. To specify the shifted parameterization (i.e., starting at x = 0), enter the command
To reset the unshifted parameterization (i.e., starting at x = 1), enter the command
This distribution is also sometimes given with
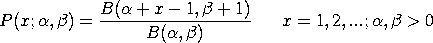
and
 and and
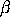 arguments
to the BGEPDF command. arguments
to the BGEPDF command.
Irwin developed the Waring distribution based on the Waring expansion. The probability mass function for the Waring distribution is
![P(x;c,a) = (c-a)*(a+x-1)!*c!/[c*(a-1)!*(c+x)!]
x = 0, 1, 2, ...; a > 0; c > a](eqns/warpdf.gif)
The Waring distribution can be computed with the shifted form of the beta-geometric distribution with the following change in parameters:
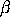 = a
= a
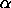 = c - a
= c - a
If a = 1, then the Waring distribution reduces to the Yule distribution. You can compute the Waring (and Yule) distributions using the BGEPDF routine with the above re-parameterization or you can use the WARPDF or YULPDF routines directly (enter HELP WARPDF or HELP YULPDF for details).
LET BETA = <value> LET Y = BETA GEOMETRIC RANDOM NUMBERS FOR I = 1 1 N
BETA GEOMETRIC PROBABILITY PLOT Y
BETA GEOMETRIC CHI-SQUARE GOODNESS OF FIT Y To obtain the first frequency and sample mean estimates and the maximum likelihood estimates of alpha and beta, enter the command
BETA GEOMETRIC MAXIMUM LIKELIHOOD Y2 X2 The maximim likelihood estimates are computed using the parameterization
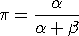
The estimates for
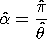
The maximim likelihood estimates are the solutions of the equations
![(n/pi) - SUM[i=1 to n][{SUM[r=1 to x(i)-1][1/(1-pi+(r-1)*theta)]}] = 0](eqns/bgemle1.gif)
Dataplot prints the estimates for both parameterizations.
You can generate estimates of
LET ALPHA2 = <value> LET BETA1 = <value> LET BETA2 = <value> BETA GEOMETRIC KS PLOT Y BETA GEOMETRIC KS PLOT Y2 X2 BETA GEOMETRIC KS PLOT Y3 XLOW XHIGH BETA GEOMETRIC PPCC PLOT Y BETA GEOMETRIC PPCC PLOT Y2 X2 BETA GEOMETRIC PPCC PLOT Y3 XLOW XHIGH The default values of alpha1 and alpha2 are 0.5 and 5, respectively. The default values for beta1 and beta2 are 0.5 and 5, respectively. Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the KS PLOT (i.e., the minimum chi-square value) is typically preferred. However, it may sometimes be useful to perform one iteration of the PPCC PLOT to obtain a rough idea of an appropriate neighborhood for the shape parameters since the minimum chi-square statistic can generate extremely large values for non-optimal values of the shape parameters. Also, since the data is integer values, one of the binned forms is preferred for these commands.
Sudhir R. Paul (2004), "Applications of the Beta Distribution" in "Handbook of the Beta Distribution", edited by Gupta and Nadarajah, Marcel-Dekker, pp. 431-436. J. O. Irwin (1963), "The Place of Mathematics in Medical and Biological Statistics", Journal of the Royal Statistical Society, Series A, 126, pp. 1-44. Johnson, Kotz, and Kemp (1992), "Univariate Discrete Distributions", Second Edition, Wiley, chapter 6.
XLIMITS 0 50
XTIC OFFSET 0.5 0.5
LINE BLANK
SPIKE ON
SPIKE THICKNESS 0.3
.
TITLE CASE ASIS
LABEL CASE ASIS
X1LABEL Number of Successes
Y1LABEL Probability Mass
.
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
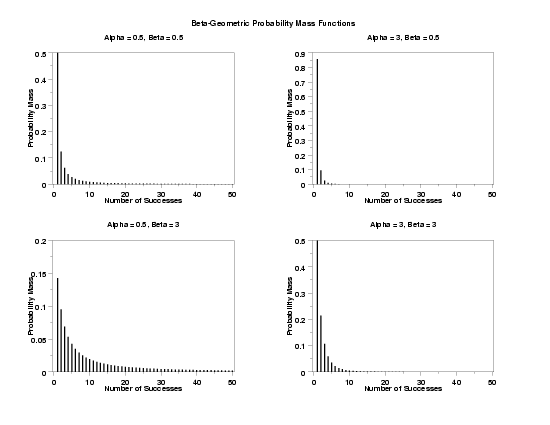
TITLE Alpha = 0.5, Beta = 0.5
PLOT BGEPDF(X,0.5,0.5) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 0.5
PLOT BGEPDF(X,3.0,0.5) FOR X = 0 1 50
.
TITLE Alpha = 0.5, Beta = 3
PLOT BGEPDF(X,0.5,3.0) FOR X = 0 1 50
.
TITLE Alpha = 3, Beta = 3
PLOT BGEPDF(X,3.0,3.0) FOR X = 0 1 50
.
END OF MULTIPLOT
.
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Beta-Geometric Probability Mass Functions
Program 2:
let alpha = 1.3
let beta = 3.1
.
let y = beta geometric random numbers for i = 1 1 200
let y3 xlow xhigh = integer frequency table y
class width 1
let amin = minimum y
let amin2 = amin - 0.5
class lower amin2
let amax = maximum y
let amax2 = amax + 0.5
class upper amax2
let y2 x2 = binned y
retain y2 x2 subset y2 > 0
.
beta geometric mle y2 x2
let alpha = alphaml
let beta = betaml
beta geometric chi-square goodness of fit test y3 xlow xhigh
.
title case asis
title offset 2
label case asis
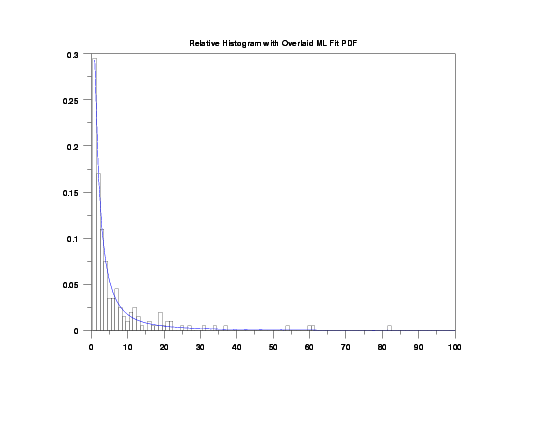
title Relative Histogram with Overlaid ML Fit PDF
xlimits 0 100
relative hist y2 x2
limits freeze
pre-erase off
line color blue
plot bgepdf(x,alpha,beta) for x = amin 1 amax
limits
pre-erase on
line color black
.
title Probability Plot for ML Fit
y1label Theoretical
x1label Data
x2label Alpha = ^alpha, Beta = ^beta
char x
line blank
beta geometric probability plot y2 x2
.
title Minimum Chi-Square Plot
y1label Chi-Square Value
x1label Beta (Curves represent values of Alpha)
x2label
line solid all
char blank all
beta geometric ks plot y3 xlow xhigh
justification center
move 50 6
text Alpha = ^shape1, Beta = ^shape2
move 50 2
text Minimum Chi-Square Value = ^minks
Date created: 8/23/2006 |