CHM

CHM (LET)

Library Function

Compute the confluent hypergeometric M function with shape parameters A and B.

The Handbook of Mathematical Functions (see the REFERENCE section below) defines 2 confluent hypergeometric functions: M and U. This command computes the M function. The CHU function computes the U function. The integral representation of the confluent hypergeometric M function is

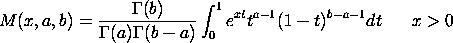
Note that the standard form is M(a,b,z). Dataplot uses M(z,a,b) to be more consistent with how other functions are entered. DATAPLOT only computes this function for real values.

Many common functions can be defined as special cases of this function (see table 13.6 in the Handbook of Mathematical Functions).

The input value must be a positive real number. The B shape parameter should not be 0 or a negative integer.

Dataplot computes these function using the CHGM routine from "Computation of Special Functions" (see the References section below).

LET <y2> = CHM(<x>,<a>,<b>)             <SUBSET/EXCEPT/FOR qualification>
where <x> is a positive number, variable, or parameter;
            <a> is a number, variable, or parameter;
            <b> is a number, variable, or parameter;
            <y2> is a variable or a parameter (depending on what <a> and <b> are) where the computed values are stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET Z = CHM(0.01,0.1,0.2)
LET Z = CHM(1,0.1,0.2)
LET Z = CHM(0.1,-1.3,0.1)

None

None

CHU	= Compute the confluent hypergeometric U function.
BETA	= Compute the complete Beta function.
BETAI	= Compute the incomplete Beta function.
GAMMA	= Compute the gamma function.
LOGGAMMA	= Compute the log gamma function.

"Computation of Special Functions", Shanjie Zhang and Jianming Jin, John Wiley and Sons, 1996, chapter 12.

"Handbook of Mathematical Functions, Applied Mathematics Series, Vol. 55", Abramowitz and Stegun, National Bureau of Standards, 1964.

Special Functions

1997/12

MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 5 5 95 95
TITLE AUTOMATIC
PLOT CHM(X,0.1,0.2) FOR X = 0 0.01 5
PLOT CHM(X,1,2) FOR X = 0 0.01 5
PLOT CHM(X,0.5,4) FOR X = 0 0.01 5
PLOT CHM(X,5,10) FOR X = 0 0.01 5
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT CONFLUENT HYPERGEOMETRIC M FUNCTIONS