DIRICHLET RANDOM NUMBER
Name:
Type:
Purpose:
Generate random numbers from a Dirichlet distribution.
Description:
The Dirichlet distribution is a generalization of the
beta distribution. To generate a matrix of Dirichlet
random numbers with n rows and k columns,
k independent vectors of length n containing
independent gamma random numbers are generated. The numbers
in each column are divided by the sum of that column.
If there are two shape parameters, the Dirichlet distribution
reduces to a Beta distribution. In addition, the marginal
distribution of each column is also a beta distribution.
Syntax:
LET <mat> = DIRICHLET RANDOM NUMBERS
<alpha> <n>
where <alpha> is a variable containing the desired shape
(> 0) parameters;
<n> is a number or parameter specifying the
desired number of observations;
and where <mat> is a matrix where the resulting Dirichlet
random numbers are stored.
Examples:
LET ALPHA = DATA 1 2 3
LET N = 1000
LET M = DIRICHLET RANDOM NUMBERS ALPHA N
Note:
Dataplot uses a Fortran translation of the
"gsl_ran_dirichlet" code (written by Gavin Crooks) from the
GNU GSL library to generate the Dirichlet random numbers.
Note:
As with univariate random numbers, the multinomial random
numbers are built on an underlying uniform random number
generator. Dataplot supports a number of different
uniform random number generators. For details, enter
HELP SET RANDOM NUMBER GENERATOR
Default:
Synonyms:
Related Commands:
|
RANDOM NUMBERS
|
= Generate random numbers for 90+ univariate
distributions.
|
|
SET RANDOM NUMBER GENERATOR
|
= Specify which univariate generator to use.
|
|
MULTIVARIATE NORM RAND NUMB
|
= Generate multivariate normal random numbers.
|
|
MULTIVARIATE T RANDOM NUMBERS
|
= Generate multivariate t random numbers.
|
|
INDEPENDENT UNIFORM RAND NUMB
|
= Generate random numbers for independent uniform
distributions.
|
|
WISHART RANDOM NUMBERS
|
= Generate random numbers for a Wishart distribution.
|
|
MULTINOMIAL RANDOM NUMBERS
|
= Generate random numbers for a multinomial
distribution.
|
Reference:
"Statistical Distributions: Third Edition", Evans, Hastings,
and Peacock, Wiley, 2000, pp. 62-64.
Applications:
Simulation, Bayesian Analysis
Implementation Date:
Program:
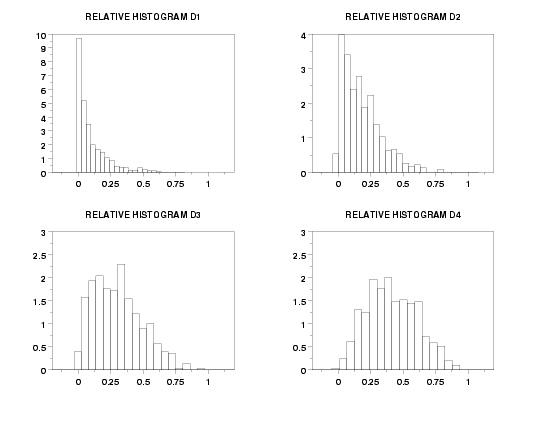
dimension 100 columns
.
let alpha = data 0.5 1.0 1.5 2.0
let n = 500
.
let d = dirichlet random numbers alpha n
.
title automatic
xlimits 0 1
xtic offset 0.2 0.2
multiplot corner coordinates 0 0 100 100
multiplot 2 2
relative histogram d1
relative histogram d2
relative histogram d3
relative histogram d4
end of multiplot
Date created: 7/7/2004
Last updated: 7/7/2004
Please email comments on this WWW page to
alan.heckert@nist.gov.
|


