

|
EWECHAZName:
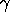 and and
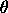 . .
![H(x,gamma,theta) = -DLOG[1-(1-EXP[-(x)**gamma])**theta]
0 < x < infinity, gamma, theta > 0](eqns/ewechaz.gif)
where
where <x> is a variable, number, or parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed exponentiated Weibull cumulative hazard value is stored; <gamma> is a positive number, parameter, or variable that specifies the first shape parameter; <theta> is a positive number, parameter, or variable that specifies the second shape parameter; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET A = EWECHAZ(A1,4,0.5) LET X2 = EWECHAZ(X1,2,1.5) LET X2 = EWECHAZ(X1,GAMMA,THETA)
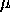 and the scale
parameter and the scale
parameter 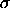 .
The general form of the cumulative hazard function can be
computed from the standard form of the cumulative hazard
function: .
The general form of the cumulative hazard function can be
computed from the standard form of the cumulative hazard
function:
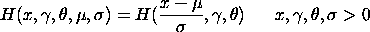
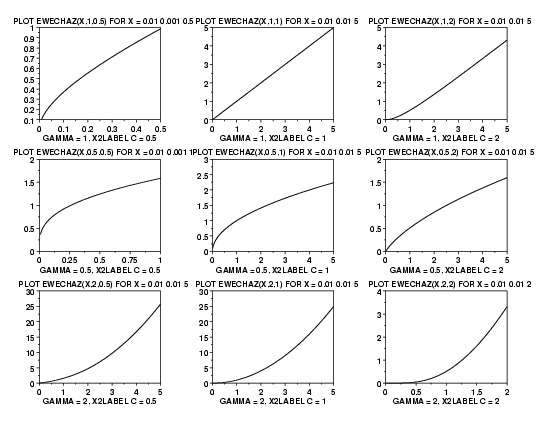
LET G = DATA 1 1 1 0.5 0.5 0.5 2 2 2
LET C = DATA 0.5 1 2 0.5 1 2 0.5 1 2
LET START = DATA 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
LET INC = DATA 0.001 0.01 0.01 0.001 0.01 0.01 0.01 0.01 0.01
LET STOP = DATA 0.5 5 5 1 5 5 5 5 2
.
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 100
TITLE AUTOMATIC
LOOP FOR K = 1 1 9
LET G1 = G(K)
LET C1 = C(K)
LET FIRST = START(K)
LET LAST = STOP(K)
LET INCT = INC(K)
X1LABEL GAMMA = ^G1, C = ^C1
PLOT EWECHAZ(X,^G1,^C1) FOR X = ^FIRST ^INCT ^LAST
END OF LOOP
END OF MULTIPLOT
Date created: 11/13/2002 |