FTPPF

FTPPF (LET)

Library Function

Compute the folded t percent point function with degrees of freedom. The degrees of freedom parameter should be a positive integer.

The folded t distribution is the absolute value of the t distribution. For details of the t distribution, enter HELP TPDF.

The folded t percent point function is computed using the t percent point as follows:

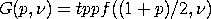
with tppf denoting the t percent point function and denoting the degrees of freedom parameter.

The folded t distribution provides an alternative to the half-normal or half-Cauchy in distributional modeling applications. A folded t with 1 degree of freedom is equivalent to a half-Cauchy and the folded t approximates the half-normal as the degrees of freedom gets large (in practice, the approximation is quite good for degrees of freedom > 30). Thus the folded t allows you to model with tails that can vary from half-normal to half-Cauchy in behavior.

LET <y> = FTPPF(<p>,<nu>)             <SUBSET/EXCEPT/FOR qualification>
where <p> is a variable, a number or a parameter in the range (0,1];
            <y> is a variable or a parameter (depending on what <p> is) where the computed folded t ppf value is stored;
            <nu> is a positive number or parameter that specifies the degrees of freedom;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = FTPPF(0.95,10)
LET Y2 = FTPPF(P1,10)
PLOT FTPPF(P,3) FOR P = 0 0.01 0.95

None

None

FTCDF	= Compute the folded t cumulative distribution function.
FTPDF	= Compute the folded t probability density function.
TPDF	= Compute the t probability density function.
STPDF	= Compute the skewed t probability density function.
HFNPDF	= Compute the half-normal probability density function.
FNRPDF	= Compute the folded normal probability density function.
HFCPDF	= Compute the half-Cauchy probability density function.

"Continuous Univariate Distributions, Volume 2", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, p. 403.

Distributional Modeling

2004/1

 
MULTIPLOT CORNER COORDINATES 0 0 100 100
MULTIPLOT SCALE FACTOR 2
MULTIPLOT 2 2
TITLE AUTOMATIC
PLOT FTPPF(P,1)  FOR X = 0  0.01  0.99
PLOT FTPPF(P,5)  FOR X = 0  0.01  0.99
PLOT FTPPF(P,10) FOR X = 0  0.01  0.99
PLOT FTPPF(P,30) FOR X = 0  0.01  0.99
END OF MULTIPLOT