

|
GETCDFName:
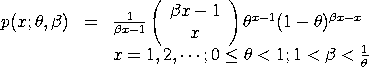
with The mean and variance of the Geeta distribution are:
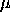 = =

The Geeta distribution is sometimes parameterized in terms
of its mean,
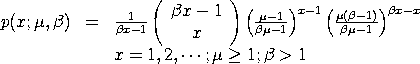
For this parameterization, the variance is
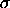 2 = 2 =
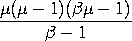
This probability mass function is also given in the form:
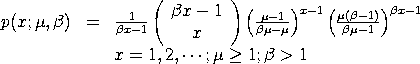
Dataplot supports both parameterizations (see the Note section below). The cumulative distribution function is computed by summing the probability mass function.
<SUBSET/EXCEPT/FOR qualification> where <x> is a positive integer variable, number, or parameter; <shape> is a number, parameter, or variable that specifies the valuie of theta (or mu); <beta> is a number, parameter, or variable that specifies the second shape parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed Geeta cdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional.
LET Y = GETCDF(X,0.3,1.6) PLOT GETCDF(X,0.3,1.6) FOR X = 1 1 20
To restore the THETA parameterization, enter the command
Consul (1990), "Geeta Distribution and its Properties", Communications in Statistics--Theory and Methods, 19, pp. 3051-3068.
set geeta definition theta
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label Probability
x1label X
.
ylimits 0 1
major ytic mark number 6
minor ytic mark number 3
xlimits 0 20
line blank
spike on
.
multiplot 2 2
.
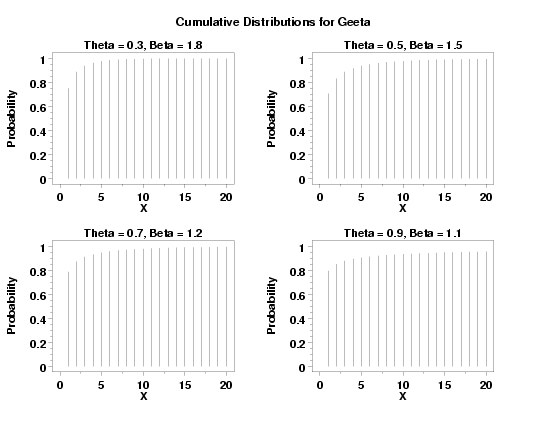
title Theta = 0.3, Beta = 1.8
plot getcdf(x,0.3,1.8) for x = 1 1 20
.
title Theta = 0.5, Beta = 1.5
plot getcdf(x,0.5,1.5) for x = 1 1 20
.
title Theta = 0.7, Beta = 1.2
plot getcdf(x,0.7,1.2) for x = 1 1 20
.
title Theta = 0.9, Beta = 1.1
plot getcdf(x,0.9,1.1) for x = 1 1 20
.
end of multiplot
.
justification center
move 50 97
text Cumulative Distributions for Geeta Distribution
Date created: 8/23/2006 |