GL5PDF

GL5PDF (LET)

Library Function

Compute the type 5 generalized logistic probability density function with shape parameter

Johnson, Kotz, and Balakrishnan (see Reference Section below) define five different versions of the generalized logistic distribution. The first four are referred to as type 1, type 2, type 3, and type 4. The fifth is a version used by Hosking. Although they do not give this version a specific name, Dataplot refers to it as either the generalized logistic type 5 or the Hosking generalized logistic distribution.

The standard form of the Hosking generalized logistic distribution has the probability density function:

The general form of the Hosking generalized logistic probability density function can be obtained by replacing x in the above formula with (x-loc)/scale.

LET <y> = GL5PDF(<x>,<alpha>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number or parameter;
            <alpha> is a number or parameter that specifies the value of the first shape parameter;
            <loc> is a number or parameter that specifies the value of the location parameter;
            <scale> is a number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized logistic type 5 pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The location and scale parameters are optional.

LET A = GL5PDF(-3,2)
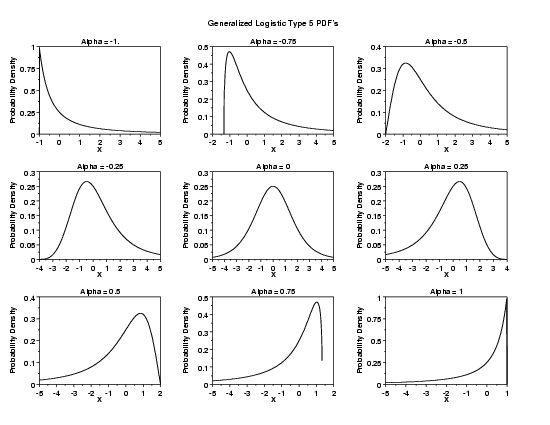
LET X2 = GL5PDF(X1,ALPHA)
PLOT GL5PDF(X,2) FOR X = -5 0.01 0.5

For this parameterization, = 0 is equivalent to the logistic distribution.

Hosking generalized logistic random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET ALPHA = <value>
LET Y = HOSKING GENERALIZED LOGISTIC RANDOM NUMBERS ...
            FOR I = 1 1 N
HOSKING GENERALIZED LOGISTIC PROBABILITY PLOT Y
HOSKING GENERALIZED LOGISTIC KOLMOGOROV SMIRNOV ...
            GOODNESS OF FIT Y
HOSKING GENERALIZED LOGISTIC CHI-SQUARE ...
            GOODNESS OF FIT Y


The following commands can be used to estimate the shape parameter for the Hosking generalized logistic distribution:

LET ALPHA1 = <value>
LET ALPHA2 = <value>
HOSKING GENERALIZED LOGISTIC PPCC PLOT Y
HOSKING GENERALIZED LOGISTIC KS PLOT Y


The default values for ALPHA1 and ALPHA2 are -2 and 2, respectively.

Bootstrap samples for these plots can be obtained with the commands

LET ALPHA1 = <value>
LET ALPHA2 = <value>
BOOTSTRAP GENERALIZED LOGISTIC TYPE 2 PLOT Y
BOOTSTRAP GENERALIZED LOGISTIC TYPE 2 KS PLOT Y


Alternatively, L-moment based estimates can be obtained with the command

GENERALIZED LOGISTIC MLE Y

Note that fitting becomes more problematic the further that the absolute value of is from zero. The greater the absolute value of , the greater the occurence of extreme values which distort the fitting procedures.

Some informal simulations showed good performance for an absolute value less than 1 (excellent for || ≤ 0.5). However, the performance rapidly declines as || gets larger than 1. For that reason, be sure to apply fitting diagnostics (probability plots, goodness of fit tests) when fitting this distribution.

None

TYPE 5 can be used as a synonym for HOSKING. For example, the following commands are equivalent:
LET Y = HOSKING GENERALIZED LOGISTIC RANDOM NUMBERS ...
            FOR I = 1 1 100
LET Y = GENERALIZED LOGISTIC HOSKING RANDOM NUMBERS ...
            FOR I = 1 1 100
LET Y = TYPE 2 GENERALIZED LOGISTIC RANDOM NUMBERS ...
            FOR I = 1 1 100
LET Y = TYPE II GENERALIZED LOGISTIC RANDOM NUMBERS ...
            FOR I = 1 1 100
LET Y = GENERALIZED LOGISTIC TYPE 2 RANDOM NUMBERS ...
            FOR I = 1 1 100
LET Y = GENERALIZED LOGISTIC TYPE II RANDOM NUMBERS ...
            FOR I = 1 1 100

GL5CDF	= Compute the generalized logistic type 5 (Hosking) cumulative distribution function.
GL5PPF	= Compute the generalized logistic type 5 (Hosking) percent point function.
GLOPDF	= Compute the generalized logistic type 1 probability density function.
GL2PDF	= Compute the generalized logistic type 2 probability density function.
GL43DF	= Compute the generalized logistic type 3 probability density function.
GL4PDF	= Compute the generalized logistic type 4 probability density function.
LOGPDF	LOGPDF = Compute the logistic probability density function.
NORPDF	= Compute the normal probability density function.
LGNPDF	= Compute the logmormal probability density function.

"Continuous Univariate Distributions - 2", 2nd. Ed., Johnson, Kotz, and Balakrishnan, John Wiley, 1994 (pp. 140-147).

Distributunial Modeling

2006/3

LET A = DATA -1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
LABEL CASE ASIS
TITLE CASE ASIS
TITLE DISPLACEMENT 2
X1LABEL X
Y1LABEL Probability Density
X1LABEL DISPLACEMENT 12
Y1LABEL DISPLACEMENT 15
.
LOOP FOR K = 1 1 9
   LET ALPHA = A(K)
   LET XSTART = -5
   LET XSTOP = 5
   IF ALPHA > 0
      LET XSTOP = 1/ALPHA
   END OF IF
   IF ALPHA < 0
      LET XSTART = 1/ALPHA
   END OF IF
   TITLE Alpha = ^ALPHA
   PLOT GL5PDF(X,ALPHA) FOR X = XSTART  0.01  XSTOP
END OF LOOP
END OF MULTIPLOT
CASE ASIS
MOVE 50 97
JUSTIFICATION CENTER
TEXT Generalized Logistic Type 5 PDF's