

|
GLDPPFName:
The original parameterization, referred to as the RS generalized Tukey-Lambda distribution, given by Ramberg and Schmeiser has the percent point function
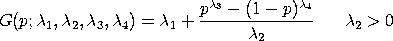
with One drawback of this parameterization is that it does not define a valid probability distribution for certain values of the parameters. Futhermore, the regions that do not define a valid probability distribution are not simple. For this reason, Friemer, Mudholkar, Kollia, and Lin developed an alternative parameterization, referred to as the FMLKL generalized Tukey-Lambda distribution, that has the percent point function
![G(p;lambda1,lambda2,lambda3,lambda4) =
lambda1 + (1/lambda2)*
[(p^lambda3-1)/lambda3 - ((1-p)^lambda4-1)/lambda4]
lambda2 > 0](eqns/gldppfg.gif)
with
Note that
If
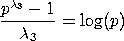
Likewise, if
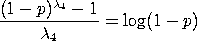
The advantage of the FMKL parameterization is that it defines
a valid probability distribution for all real values of
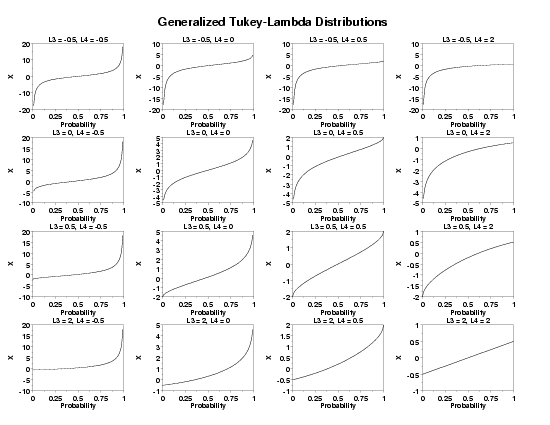
The Tukey-Lambda distribution provides a flexible model for symmetric distributions. The generalized Tukey-Lambda distribution provides a flexible model for asymmetric distributions. A few relevant properties for this distribution are:
<SUBSET/EXCEPT/FOR qualification> where <p> is a variable, number, or parameter in the range (0,1); <l3> is a number or parameter that specifies the first shape parameter; <l4> is a number or parameter that specifies the second shape parameter; <loc> is a number or parameter that specifies the location parameter; <scale> is a number or parameter that specifies the scale parameter; <y> is a variable or a parameter (depending on what <p> is) where the computed generalized Tukey-Lambda ppf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional. Note that the location and scale parameters are optional.
LET Y = GLDPPF(P,0.5,0.2) PLOT GLDPPF(P,0.5,0.2) FOR P = 0 0.01 1
LET LAMBDA4 = <value> LET Y = GENERALIZED TUKEY LAMBDA RANDOM NUMBERS ... FOR I = 1 1 N GENERALIZED TUKEY LAMBDA PROBABILITY PLOT Y GENERALIZED TUKEY LAMBDA KOLMOGOROV SMIRNOV GOODNESS OF FIT Y GENERALIZED TUKEY LAMBDA CHI-SQUARE GOODNESS OF FIT Y The following commands can be used to estimate the shape parameters for the generalized Tukey-Lambda distribution:
LET LAMBDA32 = <value> LET LAMBDA41 = <value> LET LAMBDA42 = <value> GENERALIZED TUKEY-LAMBDA PPCC PLOT Y The default values for LAMBDA31, LAMBDA32, LAMBDA41, and LAMBDA42 are -1, 5, -1 and 5, respectively. We are still resolving some issues with the GENERALIZED TUKEY LAMBDA KS PLOT command, so we recommend that you not use this for now. Alternatively, you can perform a least squares regression fit using the following commands:
LET N = SIZE Y LET PIN = UNIFORM ORDER STATISTIC MEDIANS FOR I = 1 1 N FIT Y = GLDPPF(PIN,L3,L4,ALOC,ASCALE)
Ramberg and Schmeiser (1974), "An Approximate Method for Generating Asymmetric Random Variables", Communications of the Association for Computing Machinery, 17, pp. 78-82. Ozturk and Dale (1985), "Least Squares Estimation of the Parameters of the Generalized Lambda Distribution", Technometrics, Vol. 27, No. 1, pp. 81-84. Friemer, Mudholkar, Kollia, and Lin (1988), "A Study of the Generalized Lambda Family", Communications in Statistics-Theory and Methods, 17, pp. 3547-3567. King and MacGillivray (1999), "A Starship Estimation Method for the Generalized Lambda Distributions", Australia and New Zealand Journal of Statistics, 41(3), pp. 353-374. Karian and Dudewicz (2000), Fitting Statistical Distributions: The Generalized Bootstrap Methods, New York, Chapman & Hall. Su (2005), "A Discretized Approach to Flexibly Fit Generalized Lambda Distributions to Data", Journal of Modern Applied Statistical Methods, Vol. 4, No. 2, pp. 408-424.
MULTIPLOT 4 4
MULTIPLOT SCALE FACTOR 2.5
MULTIPLOT CORNER COORDINATES 0 0 100 95
LABEL CASE ASIS
Y1LABEL X
X1LABEL Probability
X1LABEL DISPLACEMENT 16
Y1LABEL DISPLACEMENT 18
TITLE DISPLACEMENT 2
LET LAMBDA3 = DATA -0.5 0 0.5 2
LET LAMBDA4 = DATA -0.5 0 0.5 2
LOOP FOR K = 1 1 4
LET L3 = LAMBDA3(K)
LET XLOW = 0
IF L3 <= 0
LET XLOW = 0.01
END OF IF
LOOP FOR L = 1 1 4
LET L4 = LAMBDA4(L)
LET XUPP = 1
IF L4 <= 0
LET XUPP = 0.99
END OF IF
TITLE L3 = ^L3, L4 = ^L4
PLOT GLDPPF(P,L3,L4) FOR P = XLOW 0.01 XUPP
END OF LOOP
END OF LOOP
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
CASE ASIS
TEXT Generalized Tukey-Lambda Distributions
Date created: 4/14/2006 |