SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

GLSPDF

Name:
    GLSPDF (LET)
Type:
    Library Function
Purpose:
    Compute the generalized logarithmic series probability mass function.
Description:
    The generalized logarithmic series distribution has the following probability mass function:

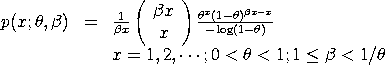
      p(x;theta,beta) = (1/(beta*x))*(beta*x x)theta**x*(1-theta)**(beta*x-x)/ (-LOG(1-theta)) x = 1, 2, ...; 0 < theta < 1; 1 <= beta < -1/theta

    with theta and beta denoting the shape parameters and Gamma denoting the gamma function (enter HELP GAMMA for details).

    Note that there are several distributions in the literature that are called the generalized logarithmic series distribution. We are using the definition given in Consul and Famoye (see References below).

Syntax:
    LET <y> = GLSPDF(<x>,<theta>,<beta>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a positive integer variable, number, or parameter;
                <theta> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
                <beta> is a number, parameter, or variable that specifies the second shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed generalized logarithmic series pdf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = GLSPDF(3,0.5,1.4)
    LET Y = GLSPDF(X,0.3,1.6)
    PLOT GLSPDF(X,0.3,1.6) FOR X = 1 1 20
Note:
    For a number of commands utilizing the generalized logarithmic series distribution, it is convenient to bin the data. There are two basic ways of binning the data.

    1. For some commands (histograms, maximum likelihood estimation), bins with equal size widths are required. This can be accomplished with the following commands:

        LET AMIN = MINIMUM Y
        LET AMAX = MAXIMUM Y
        LET AMIN2 = AMIN - 0.5
        LET AMAX2 = AMAX + 0.5
        CLASS MINIMUM AMIN2
        CLASS MAXIMUM AMAX2
        CLASS WIDTH 1
        LET Y2 X2 = BINNED

    2. For some commands, unequal width bins may be helpful. In particular, for the chi-square goodness of fit, it is typically recommended that the minimum class frequency be at least 5. In this case, it may be helpful to combine small frequencies in the tails. Unequal class width bins can be created with the commands

        LET MINSIZE = <value>
        LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y

      If you already have equal width bins data, you can use the commands

        LET MINSIZE = <value>
        LET Y3 XLOW XHIGH = COMBINE FREQUENCY TABLE Y2 X2

      The MINSIZE parameter defines the minimum class frequency. The default value is 5.

Note:
    You can generate generalized logarithmic series random numbers, probability plots, and chi-square goodness of fit tests with the following commands:

      LET N = VALUE
      LET THETA = <value>
      LET BETA = <value>
      LET Y = GENERALIZED LOGARITHMIC SERIES ...
      RANDOM NUMBERS FOR I = 1 1 N

      GENERALIZED LOGARITHMIC SERIES PROBABILITY PLOT Y
      GENERALIZED LOGARITHMIC SERIES PROBABILITY PLOT Y2 X2
      GENERALIZED LOGARITHMIC SERIES PROBABILITY PLOT ...
                  Y3 XLOW XHIGH

      GENERALIZED LOGARITHMIC SERIES CHI-SQUARE ...
                  GOODNESS OF FIT Y
      GENERALIZED LOGARITHMIC SERIES CHI-SQUARE ...
                  GOODNESS OF FIT Y2 X2
      GENERALIZED LOGARITHMIC SERIES CHI-SQUARE ...
                  GOODNESS OF FIT Y3 XLOW XHIGH

    To obtain the method of moment estimates, the mean and ones frequency estimates, and the maximum likelihood estimates of theta and beta, enter the command

      GENERALIZED LOGARITHMIC SERIES MAXIMUM LIKELIHOOD Y
      GENERALIZED LOGARITHMIC SERIES MAXIMUM LIKELIHOOD Y2 X2

    The method of moment estimate of theta is the solution of the equation

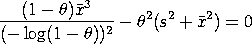
      (1-theta)*xbar^3/(-LOG(1-theta)) - theta^2*(s^2+xbar^2) = 0

    with xbar and s2 denoting the sample mean and the sample variance, respectively.

    The moment estimate of beta is then

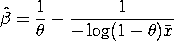
      betahat = 1/theta - 1/(-LOG(1-theta)*xbar)

    The proportion of ones and sample mean method estimate of theta is the solution of the equation

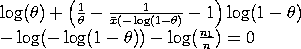
      LOG(theta) + {1/(theta) - 1/(xbar*(-LOG(1-theta)) - 1}*LOG(1-theta) - LOG(-LOG(1-theta)) - LOG(n(1)/n) = 0

    with xbar, n1, and n denoting the sample mean, the sample frequency of X = 1, and the total sample size, respectively.

    The proportion of ones and sample mean estimate of beta is then

      betahat = 1/theta - 1/(-LOG(1-theta)*xbar)

    The maximum likelihood estimates of theta and beta are the solution to the following equations:

    with k, n, and nx denoting the number of classes, the total sample size, and the count for the xth class, respectively.

    You can generate estimates of theta and beta based on the maximum ppcc value or the minimum chi-square goodness of fit with the commands

      LET THETA1 = <value>
      LET THETA2 = <value>
      LET BETA1 = <value>
      LET BETA2 = <value>
      GENERALIZED LOGARITHMIC SERIES KS PLOT Y
      GENERALIZED LOGARITHMIC SERIES KS PLOT Y2 X2
      GENERALIZED LOGARITHMIC SERIES KS PLOT ...
                  Y3 XLOW XHIGH
      GENERALIZED LOGARITHMIC SERIES PPCC PLOT Y
      GENERALIZED LOGARITHMIC SERIES PPCC PLOT Y2 X2
      GENERALIZED LOGARITHMIC SERIES PPCC PLOT ...
                  Y3 XLOW XHIGH

    The default values of theta1 and theta2 are 0.05 and 0.95, respectively. The default values for beta1 and beta2 are 1.05 and 5, respectively. Note that values of beta that do not lie in the interval 1 ≤ beta ≤ 1/theta are skipped.

    Due to the discrete nature of the percent point function for discrete distributions, the ppcc plot will not be smooth. For that reason, if there is sufficient sample size the KS PLOT (i.e., the minimum chi-square value) is typically preferred. However, it may sometimes be useful to perform one iteration of the PPCC PLOT to obtain a rough idea of an appropriate neighborhood for the shape parameters since the minimum chi-square statistic can generate extremely large values for non-optimal values of the shape parameters. Also, since the data is integer values, one of the binned forms is preferred for these commands.

Default:
    None
Synonyms:
    None
Related Commands:
    GLSCDF = Compute the generalized logarithmic series cumulative distribution function.
    GLSPPF = Compute the generalized logarithmic series percent point function.
    DLGPDF = Compute the logarithmic series probability mass function.
    YULPDF = Compute the Yule probability mass function.
    ZETPDF = Compute the Zeta probability mass function.
    BGEPDF = Compute the beta geometric probability mass function.
    POIPDF = Compute the Poisson probability mass function.
    BINPDF = Compute the binomial probability mass function.
    INTEGER FREQUENCY TABLE = Generate a frequency table at integer values with unequal bins.
    COMBINE FREQUENCY TABLE = Convert an equal width frequency table to an unequal width frequency table.
    KS PLOT = Generate a minimum chi-square plot.
    MAXIMUM LIKELIHOOD = Perform maximum likelihood estimation for a distribution.
Reference:
    Consul and Famoye (2006), "Lagrangian Probability Distribution", Birkhauser, chapter 11.

    Famoye (1995), "On Certain Methods of Estimation for Generalized Logarithmic Series Distribution", Journal of Applied Statistical Sciences, 2, pp. 103-117.

Applications:
    Distributional Modeling
Implementation Date:
    2006/8
Program 1: 
     
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
y1label Probability Mass
x1label X
.
ylimits 0 1
major ytic mark number 6
minor ytic mark number 3
xlimits 0 20
line blank
spike on
.
multiplot 2 2
.
title Theta = 0.3, Beta = 1.8
plot glspdf(x,0.3,1.8) for x = 1 1 20
.
title Theta = 0.5, Beta = 1.5
plot glspdf(x,0.5,1.5) for x = 1 1 20
.
title Theta = 0.7, Beta = 1.2
plot glspdf(x,0.7,1.2) for x = 1 1 20
.
title Theta = 0.9, Beta = 1.1
plot glspdf(x,0.9,1.1) for x = 1 1 20
.
end of multiplot
.
justification center
move 50 97
text Probability Mass Functions for Generalized Logarithmic Series
    plot generated by sample program

Program 2: 
     
LET THETA = 0.7
LET BETA  = 1.2
LET Y = GENERALIZED LOGARITHMIC SERIES RANDOM NUMBERS ...
        FOR I = 1 1 500
.
LET Y3 XLOW XHIGH = INTEGER FREQUENCY TABLE Y
CLASS LOWER 0.5
CLASS WIDTH 1
LET AMAX = MAXIMUM Y
LET AMAX2 = AMAX + 0.5
CLASS UPPER AMAX2
LET Y2 X2 = BINNED Y
.
GENERALIZED LOGARITHMIC SERIES MLE Y
RELATIVE HISTOGRAM Y2 X2
LIMITS FREEZE
PRE-ERASE OFF
LINE COLOR BLUE
PLOT GLSPDF(X,THETAML,BETAML) FOR X = 0  1  AMAX
LIMITS
PRE-ERASE ON
LINE COLOR BLACK
LET THETA = THETAML
LET BETA  = BETAML
GENERALIZED LOGARITHMIC SERIES CHI-SQUARE GOODNESS OF FIT ...
    Y3 XLOW XHIGH
CASE ASIS
JUSTIFICATION CENTER
MOVE 50 97
TEXT Theta = ^THETAML, Beta = ^BETAML
MOVE 50 93
TEXT Minimum Chi-Square = ^STATVAL, 95% CV = ^CUTUPP95
.
LABEL CASE ASIS
X1LABEL Theta
Y1LABLE Minimum Chi-Square
GENERALIZED LOGARITHMIC SERIES KS PLOT Y3 XLOW XHIGH
LET THETA = SHAPE1
LET BETA  = SHAPE2
GENERALIZED LOGARITHMIC SERIES CHI-SQUARE GOODNESS OF FIT ...
    Y3 XLOW XHIGH
JUSTIFICATION CENTER
MOVE 50 97
TEXT Theta = ^THETA, Beta = ^BETA
MOVE 50 93
TEXT Minimum Chi-Square = ^MINKS, 95% CV = ^CUTUPP95
    plot generated by sample program 
     
                   CHI-SQUARED GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            GENERALIZED LOGARITHMIC SERIES
  
 SAMPLE:
    NUMBER OF OBSERVATIONS      =      500
    NUMBER OF NON-EMPTY CELLS   =       15
    NUMBER OF PARAMETERS USED   =        2
  
 TEST:
 CHI-SQUARED TEST STATISTIC     =    8.849097
    DEGREES OF FREEDOM          =       12
    CHI-SQUARED CDF VALUE       =    0.284237
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       18.54935               ACCEPT H0
             5%       21.02607               ACCEPT H0
             1%       26.21697               ACCEPT H0
    plot generated by sample program 
                       CHI-SQUARED GOODNESS-OF-FIT TEST
  
 NULL HYPOTHESIS H0:      DISTRIBUTION FITS THE DATA
 ALTERNATE HYPOTHESIS HA: DISTRIBUTION DOES NOT FIT THE DATA
 DISTRIBUTION:            GENERALIZED LOGARITHMIC SERIES
  
 SAMPLE:
    NUMBER OF OBSERVATIONS      =      500
    NUMBER OF NON-EMPTY CELLS   =       15
    NUMBER OF PARAMETERS USED   =        2
  
 TEST:
 CHI-SQUARED TEST STATISTIC     =    8.898336
    DEGREES OF FREEDOM          =       12
    CHI-SQUARED CDF VALUE       =    0.288412
  
    ALPHA LEVEL         CUTOFF              CONCLUSION
            10%       18.54935               ACCEPT H0
             5%       21.02607               ACCEPT H0
             1%       26.21697               ACCEPT H0

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].