GMCPDF

GMCPDF (LET)

Library Function

Compute the generalized McLeish probability density function.

The standard form of the generalized McLeish distribution has the following probability density function:

with K(.) denoting the modified Bessel function of the of the second kind of order and denoting the gamma function.

The standard generalized McLeish distribution can be generalized with location and scale parameters in the usual way.

LET <y> = GMCPDF(<x>,<alpha>,<a>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter;
            <alpha> is a positive number of parameter that specifies the value of the first shape parameter;
            <a> is a positive number of parameter that specifies the value of the second shape parameter;
            <loc> is an optional number or parameter that specifies the value of the location parameter;
            <scale> is an optional positive number or parameter that specifies the value of the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed generalized McLeish pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET Y = GMCPDF(3,1.5,0.8)
LET Y = GMCPDF(X1,ALPHA,A)
PLOT GMCPDF(X,ALPHA,A) FOR X = -10 0.01 10

DATAPLOT uses the routine DBESK from the SLATEC Common Mathematical Library to compute the modified Bessel function of the second kind. SLATEC is a large set of high quality, portable, public domain Fortran routines for various mathematical capabilities maintained by seven federal laboratories.

To generate generalized McLeish random numbers, enter the commands
LET ALPHA = <value>
LET A = <value>
LET Y = GENERALIZED MCLEISH RANDOM NUMBERS FOR I = 1 1 N


To generate a generalized McLeish probability plot or a McLeish Kolmogorov-Smirnov or chi-square goodness of fit test, enter the following commands

LET ALPHA = <value>
LET A = <value>
GENERALIZED MCLEISH PROBABILITY PLOT Y
GENERALIZED MCLEISH KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
GENERALIZED MCLEISH CHI-SQUARE GOODNESS OF FIT Y


To generate a PPCC or Kolmogorov-Smirnov plot, enter the following commands

LET ALPHA1 = <value>
LET ALPHA2 = <value>
LET A1 = <value>
LET A2 = <value>
GENERALIZED MCLEISH PPCC PLOT Y
GENERALIZED MCLEISH KS PLOT Y


The default values for ALPHA1 and ALPHA2 are 0.5 and 10 and the default values for A1 and A2 are -0.8 and 0.8.

None

None

GMCCDF	= Compute the generalized McLeish cumulative distribution function.
GMCPPF	= Compute the generalized McLeish percent point function.
MCLPDF	= Compute the McLeish probability density function.
GALPDF	= Compute the generalized asymmetric Laplace cumulative distribution function.
GIGPDF	= Compute the generalized inverse Gaussian probability density function.
BEIPDF	= Compute the Bessel I-function probability density function.
BEKPDF	= Compute the Bessel K-function probability density function.

Johnson, Kotz, and Balakrisnan, "Continuous Univariate Distributions--Volume I", Second Edition, Wiley, 1994, pp. 50-53.

Distributional Modeling

8/2004

 
Y1LABEL Probability
X1LABEL X
LABEL CASE ASIS
TITLE CASE ASIS
CASE ASIS
Y1LABEL DISPLACEMENT 16
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
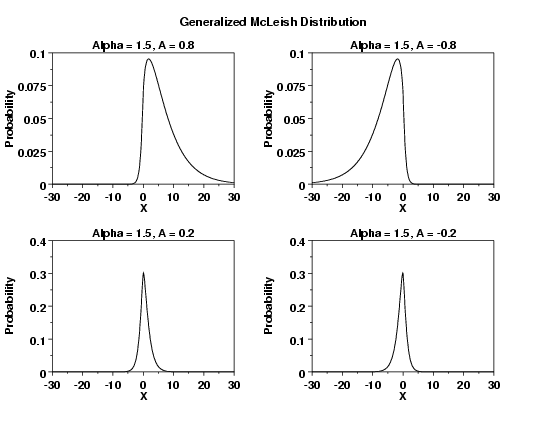
LET A = 0.8
TITLE Alpha = 1.5, A = 0.8
PLOT GMCPDF(X,1.5,A) FOR X = -30  0.1 30
LET A = -0.8
TITLE Alpha = 1.5, A = -0.8
PLOT GMCPDF(X,1.5,A) FOR X = -30  0.1 30
LET A = 0.2
TITLE Alpha = 1.5, A = 0.2
PLOT GMCPDF(X,1.5,A) FOR X = -30  0.1 30
LET A = -0.2
TITLE Alpha = 1.5, A = -0.2
PLOT GMCPDF(X,1.5,A) FOR X = -30  0.1 30
END OF MULTIPLOT
MOVE 50 97
JUSTIFICATION CENTER
TEXT Generalized McLeish Distribution