

|
KUMPDFName:
 and and
 . .
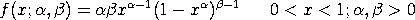
with This distribution can be extended with lower and upper bound parameters. If a and b denote the lower and upper bounds, respectively, then the location and scale parameters are:
scale = b - a The general form of the distribution can then be found by using the relation
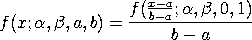
This distribution has been proposed as a more tractable alternative to the beta distribution.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable containing values in the interval (a,b); <y> is a variable or a parameter (depending on what <x> is) where the computed Kumaraswamy pdf value is stored; <alpha> is a positive number, parameter, or variable that specifies the first shape parameter; <beta> is a positive number, parameter, or variable that specifies the second shape parameter; <a> is a number, parameter, or variable that specifies the lower limit; <b> is a number, parameter, or variable that specifies the upper limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. If <a> and <b> are omitted, they default to 0 and 1, respectively.
LET Y = KUMPDF(X,0.5,2) PLOT KUMPDF(X,2,3) FOR X = 0 0.01 1
LET BETA = <value> LET A = <value> LET B = <value> LET Y = KUMARASWAMY RANDOM NUMBERS FOR I = 1 1 N KUMARASWAMY PROBABILITY PLOT Y KUMARASWAMY PROBABILITY PLOT Y2 X2 KUMARASWAMY PROBABILITY PLOT Y3 XLOW XHIGH KUMARASWAMY KOLMOGOROV SMIRNOV GOODNESS OF FIT Y KUMARASWAMY CHI-SQUARE GOODNESS OF FIT Y2 X2 KUMARASWAMY CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH The following commands can be used to estimate the alpha and beta shape parameters for the Kumaraswamy distribution:
LET ALPHA2 = <value> LET BETA1 = <value> LET BETA2 = <value> KUMARASWAMY PPCC PLOT Y KUMARASWAMY PPCC PLOT Y2 X2 KUMARASWAMY PPCC PLOT Y3 XLOW XHIGH KUMARASWAMY KS PLOT Y KUMARASWAMY KS PLOT Y2 X2 KUMARASWAMY KS PLOT Y3 XLOW XHIGH The default values for ALPHA1 and ALPHA2 are 0.5 and 10. The default values for BETA1 and BETA2 are 0.5 and 10. The probability plot can then be used to estimate the lower and upper limits (lower limit = PPA0, upper limit = PPA0 + PPA1). The following options may be useful for these commands.
CASE ASIS
LABEL CASE ASIS
TITLE CASE ASIS
TITLE OFFSET 2
.
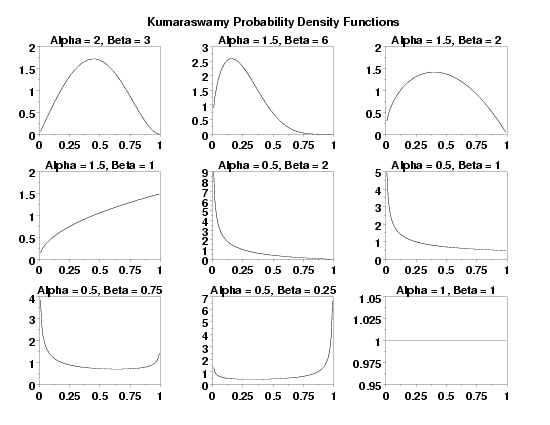
MULTIPLOT 3 3
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 3
.
LET ALPHA = 2
LET BETA = 3
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 1.5
LET BETA = 6
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 1.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 1.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 0.5
LET BETA = 2
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 0.5
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 0.5
LET BETA = 0.75
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 0.5
LET BETA = 0.25
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
LET ALPHA = 1
LET BETA = 1
TITLE Alpha = ^alpha, Beta = ^beta
PLOT KUMPDF(X,ALPHA,BETA) FOR X = 0.01 0.01 0.99
.
END OF MULTIPLOT
.
JUSTIFICATION CENTER
MOVE 50 97
TEXT Kumaraswamy Probability Density Functions
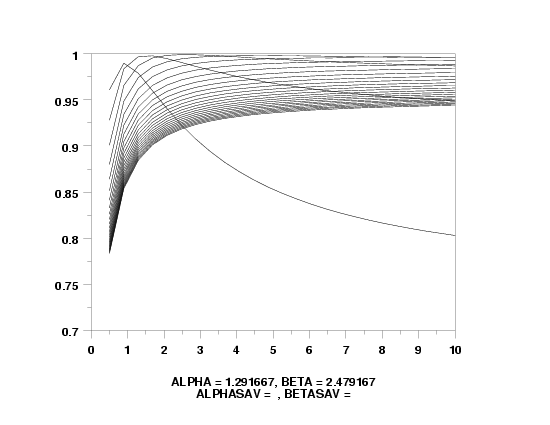
Program 2:
let alpha = 1.2
let beta = 2.6
let alphasv = alpha
let betasv = beta
.
let y = kuaraswamy rand numb for i = 1 1 200
.
kumaraswamy ppcc plot y
justification center
move 50 6
let alpha = shape1
let beta = shape2
text Alpha = ^alpha, Beta = ^beta
move 50 3
text Alphasav = ^alphsav, Betasav = ^betasav
.
char x
line blank
kumaraswamy probability plot y
move 50 6
let lowlim = ppa0
let upplim = ppa0 + ppa1
text Lower Limit = ^lowlim, Upper Limit = ^upplim
move 50 3
text PPCC = ^ppcc
char blank
line solid
let ksscale = upplim
kumaraswamy kolm smir goodness of fit y
Date created: 11/27/2007 |