

|
LBECDFName:
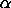 , ,
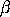 ,
c, and d. ,
c, and d.
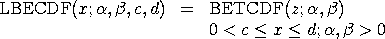
with
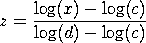
The log beta distribution can be generalized with location and scale parameters in the usual way.
<SUBSET/EXCEPT/FOR qualification> where <x> is a number, parameter, or variable; <alpha> is a number, parameter, or variable that specifies the first shape parameter; <beta> is a number, parameter, or variable that specifies the second shape parameter; <c> is a number, parameter, or variable that specifies the third shape parameter; <d> is a number, parameter, or variable that specifies the fourth shape parameter; <loc> is a number, parameter, or variable that specifies the optional location parameter; <scale> is a number, parameter, or variable that specifies the optional scale parameter; <y> is a variable or a parameter (depending on what <x> is) where the computed log beta cdf value is stored; and where the <SUBSET/EXCEPT/FOR qualification> is optional. The location and scale parameters are optional (the default values are zero and one, respectively).
LET Y = LBECDF(X,ALPHA,BETA,C,D) PLOT LBECDF(X,6,6,1,3) FOR X = 1.01 0.01 2.99
title displacement 2
y1label displacement 17
x1label displacement 12
case asis
title case asis
label case asis
y1label Probability
x1label X
.
let c = 1
let d = 3
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
multiplot 2 2
.
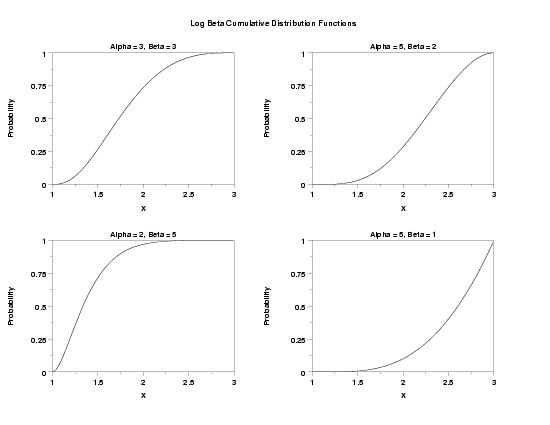
title Alpha = 3, Beta = 3
plot lbecdf(x,3,3,c,d) for x = 1.01 0.01 2.99
.
title Alpha = 5, Beta = 2
plot lbecdf(x,5,2,c,d) for x = 1.01 0.01 2.99
.
title Alpha = 2, Beta = 5
plot lbecdf(x,2,5,c,d) for x = 1.01 0.01 2.99
.
title Alpha = 5, Beta = 1
plot lbecdf(x,5,1,c,d) for x = 1.01 0.01 2.99
.
end of multiplot
.
justification center
move 50 97
text Log Beta Cumulative Distribution Functions
Date created: 8/23/2006 |