SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

L MOMENTS

Name:
    L MOMENTS (LET)
Type:
    Let Subcommand
Purpose:
    Compute the sample L-moment ratios of a variable.
Description:
    Given a random variable X with a cumulative distribution function F, the probability weighted moments are defined to be:

      M(p,r,s) = E[X**p{F(X)}**r{1 - F(X)}**s]

    Two special cases are

      alpha(r) = M(1,0,r) = E[X{1 - F(X)}**r]

      beta(r) = M(1,r,0) = E[X{F(X)}**r]

    The L-moments are defined as

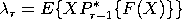
      lambda(r) = E{X*P*(r-1){F(X)}}

    with P*(r)(.) denoting the rth shifted Legendre ploynomials. The L-moment estimators are linear combinations of order statistics.

    L-moments are related to probability weighted moments by the equation

      lamda(r+1) - SUM[k=0 to r][p*(r,k)*beta(k)]

    where

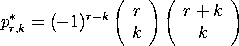
      p*(r,k) = (-1)**(r-k)*(r k)*(r+k k)

    with (r k) denoting the binomal coefficient.

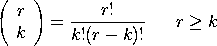
      (r k) = r!*/(k!*(r-k)!)

    The L-moment ratios are defined to be

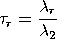
      tau(r) = lambda(r)/lambda(2)

    This command returns the L-moment estimates for orders 1 and 2 and L-moment ratios for higher orders.

    For an ordered sample x1:n <= x2:n <= ... <= xn:n, unbiased estimators of

      a(r) = (1/n)*SUM[j=1 to n][(n-j)*(n-j-1)* ... *(n-j-r+1)/ ((n-1)*(n-2)* ... *(n-r))]*xj:n

      alt="b(r)

      l(r+1) = SUM[k=0 to r][p*(r,k)*b(k)

    The primary use of probability weighted moments and L-moments is in the estimation of parameters for a probability distribution. Estimates based on probability weighted moments and L-moments are generally superior to standard moment-based estimates. The L-moment estimators have some desirable properties for parameter estimation. In particular, they are robust with respect to outliers and their small sample bias tends to be small. L-moment estimators can often be used when the maximum likelihood estimates are unavailable, difficult to compute, or have undesirable properties. They may also be used as starting values for maximum likelihood estimates.

    Estimation methods based on L-moments are discussed in the papers listed in the Reference section below (Dataplot generates L-moment based estimates for the maximum likelihood estimates for the generalized Pareto and the generalized extreme value distributions).

Syntax:
    LET <y> = L MOMENTS <x> <nmom>
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is the response variable;
                <nmom> is the number of L-moments that will be generated;
                <y> is a variable where the computed L-moments are saved;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET XMOM = L MOMENTS Y 5
    LET XMOM = L MOMENTS Y 4 SUBSET Y > 0
Note:
    Dataplot computes L-moments using the SAMLMU routine written by Hoskings and documented in "Research Report: Fortran Routines for use with the Method of L-Moments" (see the Reference section below).

    Hoskings software provides L-moment estimators for 11 different distributions. Dataplot currently implements the L-moment estimates for the generalized Pareto and generalized extreme value distributions. To obtain these estimates, enter the commands

      GENERALIZED PARETO MAXIMUM LIKELIHOOD Y
      GENERALIZED EXTREME VALUE MAXIMUM LIKELIOHOOD Y

    We plan to implement the L-moment estimators for additional distributions in future releases of Dataplot.

Default:
    If the <nmom> parameter is omitted from the command, the first four sample L-moments are computed.
Synonyms:
    None
Related Commands: References:
    "Research Report: Fortran Routines for use with the Method of L-Moments", J. R. M. Hosking, IBM Research Division, T. J. Watson Research Center, Yorktown Heights, NY 10598, 6/2000.

    "L-moments: Analysis and Estimation of Distribution using Linear Combinations of Order Statistics", Hoskings, Journal of the Royal Statistical Society, Series B, 52, 1990, pp. 105-124.

    "The Estimation of Extreme Quantiles of Wind Velocity Using L-Moments in the Peaks-Over-Threshold Approach", Pandey, Van Gelder, and Vrijling, Structural Safety, 23, 2001, pp. 179-192.

    "Probability Weighted Moments: Definition and Relation to Parameters of Several Distributions Expressable in Inverse Form", Greenwood, Landwehr, Matalas, and Wallis, Water Resources Research, 15, 1979, 1049-1054.

    "Estimation of the Generalized Extreme Value Distribution by the Method of Probability-Weighte Moments", Hosking, Wallis, and Wood, Technometrics, 27, 1985, 251-261.

    "Probability Weighted Moments Compared with Some Traditional Techniques in Estimating Gumbel Parameters and Quantiles", Landwehr, Matalas, Wallis, Water Resources Research, 15, (1979a), 1055-1064.

    "Extreme Value and Related Models with Applications in Engineering and Science", Castillo, Hadi, Balakrishnan, and Sarabia, Wiley, 2005, pp. 117-119.

Applications:
    Distributional Modeling
Implementation Date:
    2005/6
Program: 
     
LET GAMMA = -0.3
LET Y = GENERALIZED PARETO RANDOM NUMBERS FOR I = 1 1 100
LET Y = 5*Y
LET NMOM = 3
LET XMOM = L MOMENTS Y NMOM
PRINT XMOM
GENERALIZED PARETO MLE Y
    The following output is generated 
     

 VARIABLES--XMOM    

   0.4160070E+01
  -0.3669064E-01
  -0.4920776E+00
 

             GENERALIZED PARETO PARAMETER ESTIMATION:
  
 SUMMARY STATISTICS:
 NUMBER OF OBSERVATIONS                     =      100
 SAMPLE MEAN (ALL DATA)                     =    4.160070
 SAMPLE VARIANCE (ALL DATA)                 =    9.603471
 SAMPLE MINIMUM                             =   0.7464492E-02
 SAMPLE MAXIMUM                             =    12.82312
 USER-SPECIFIED THRESHOLD                   =    0.000000
  
 METHOD OF MOMENTS:
 (VALID IF SHAPE PARAMETER < 1)
 SAMPLE MEAN (AFTER SUBTRACT LOCATION)      =    4.152607
 SAMPLE VARIANCE (AFTER SUBTRACT LOCATION)  =    9.603471
 ESTIMATE OF LOCATION                       =   0.7463745E-02
 ESTIMATE OF SCALE                          =    5.804547
 ESTIMATE OF GAMMA                          =  -0.3978080
 VARIANCE OF GAMMA                          =   0.1448942E-01
 VARIANCE OF SCALE                          =   0.6819228
 COVARIANCE OF GAMMA AND SCALE              =   0.8959930E-01
  
 L-MOMENTS:
 (L-MOMENT ESTIMATES WORK BEST FOR
 VALUES OF SHAPE PARAMETER IN (-0.5,0.5))
 FIRST SAMPLE L-MOMENT                      =    4.160070
 SECOND SAMPLE L-MOMENT                     =    1.718239
 THIRD SAMPLE L-MOMENT                      =   0.2119006
 ESTIMATE OF LOCATION                       =   0.2070879
 ESTIMATE OF SCALE                          =    5.141252
 ESTIMATE OF SHAPE                          =  -0.3006007
  
 ELEMENTAL PERCENTILE METHOD:
 ESTIMATE OF LOCATION                       =   0.7463745E-02
 ESTIMATE OF SCALE                          =    5.473905
 ESTIMATE OF GAMMA                          =  -0.4396029
  
 MAXIMUM LIKELIHOOD:
 (MAXIMUM LIKELIHOOD ESTIMATES DO
 NOT EXIST IF SHAPE PARAMTER < -1
 AND MAY PERFORM POORLY IF < -0.5)
 ESTIMATE OF LOCATION                       =   0.7463745E-02
 ESTIMATE OF SCALE                          =    3.383862
 ESTIMATE OF GAMMA                          =  -0.2713313
 VARIANCE OF GAMMA                          =   0.1616283E-01
 VARIANCE OF SCALE                          =   0.2911481
 COVARIANCE OF GAMMA AND SCALE              =   0.4302010E-01
  
  
 NOTE: FOR THE GENERALIZED PARETO DISTRIBUTION, LARGE SAMPLE SIZES
       MAY BE REQUIRED FOR THE NORMAL APPROXIMATIONS TO BE ACCURATE (E.G., > 500).
  
 CONFIDENCE INTERVAL FOR SCALE PARAMETER
  
                        NORMAL APPROXIMATION
    CONFIDENCE           LOWER         UPPER
    VALUE (%)            LIMIT         LIMIT
 -------------------------------------------
      50.000           3.01992       3.74780
      75.000           2.76315       4.00457
      90.000           2.49633       4.27139
      95.000           2.32630       4.44142
      99.000           1.99399       4.77373
      99.900           1.60836       5.15936
  
 CONFIDENCE INTERVAL FOR SHAPE PARAMETER
  
                        NORMAL APPROXIMATION
    CONFIDENCE           LOWER         UPPER
    VALUE (%)            LIMIT         LIMIT
 -------------------------------------------
      50.000          -.357081      -.185581
      75.000          -.417579      -.125084
      90.000          -.480447      -.622159E-01
      95.000          -.520508      -.221549E-01
      99.000          -.598805      0.561420E-01
      99.900          -.689665      0.147002

    Date created: 1/6/2006
    Last updated: 1/6/2006
    Please email comments on this WWW page to alan.heckert@nist.gov.