NUMERICAL DERIVATIVE

NUMERICAL DERIVATIVE (LET)

Let Subcommand

Compute the derivative for a univariate function numerically.

The DERIVATIVE LET subcommand computes a derivative by first determining the analytic derivative function and then evaluating that function at the requested point (or points). However, Dataplot only computes the analytic derivative for a limited number of basic functions (including combinations of these functions).

If Dataplot cannot compute the analytic derivative of a function, you can use the NUMERICAL DERIVATIVE instead.

This command is limited to univariate functions (i.e., it does not compute partial derivatives).

LET <resp> = NUMERICAL DERIVATIVE <function> WRT <var>
where <function> is the name of a previously defined function;
            <var> is the name of the variable with respect to which the derivative is taken;
and    <resp> is a variable of the same length as <var> where the evaluated derivatives are stored.

With this syntax, the derivative variable (<var>) must be defined for one or more points. The derivative is calculated at each of these points and the resulting value is put in the corresponding element of .

LET <resp> = NUMERICAL DERIVATIVE <function> WRT <var>
            FOR <var> = <value>
where <function> is the name of a previously defined function;
            <var> is the name of the variable with respect to which the derivative is taken;
            <value> is a number or parameter at which the derivative is to be evaluated;
and    <resp> is a parameter of length 1 where the evaluated derivative is stored.

This syntax is similar to Syntax 1. However, the FOR clause identifies a single point at which the derivative is to be evaluated and <var> does not need to be pre-specified.

LET X = SEQUENCE -5 0.1 5
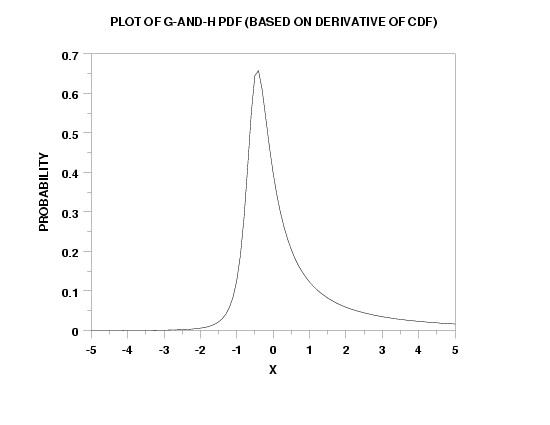
LET XDERV = NUMERICAL DERIVATIVE 3*X**2 -8*X + 4 WRT X


LET X = SEQUENCE -5 0.1 5
LET FUNCTION F = 3*X**2 -8*X + 4
LET Y = NUMERICAL DERIVATIVE F WRT X
LET A = NUMERICAL DERIVATIVE F WRT X FOR X = 2.3

DATAPLOT uses the DIFF routine written by David Kahaner (formerly of NIST) to compute the numeric derivative. This routine uses Neville's process to extrapolate from a sequence of simple polynomial approximations based on interpolating points distributed symmetrically about the point at which the derivative is to be computed.

None

None

DERIVATIVE	= Compute the analytic derivative of a function.
INTEGRAL	= Compute the integral of a function.
ROOTS	= Compute the roots of a function.
RUNGE KUTTA	= Runge Kutta differential equation solver.
INTERPOLATE	= Interpolate a function.

Consult any standard Calculus textbook.

Mathematics

2004/1

 
.
.  Compute the PDF of a G-and-H distribution by computing the
.  derivative of the G-and-H CDF function.
.
LET G = 1.5
LET H = 0.3
LET FUNCTION F = GHCDF(X,G,H)
LET X = SEQEUNCE -5 0.1 5
LET Y = NUMERICAL DERIVATIVE F WRT X
Y1LABEL PROBABILITY
X1LABEL X
TITLE PLOT OF G-AND-H PDF (BASED ON DERIVATIVE OF CDF)
PLOT Y VS X