PA2PDF

PA2PDF (LET)

Library Function

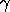Compute the Pareto probability density function of the second kind with shape parameters and a.

The standard form of the Pareto probability density function of the second kind is:

with and a denoting the shape parameters. The a parameter is optional and has a default value of 1.

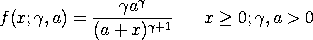
The Pareto distribution of the second kind is sometimes referred to as the Lomax distribution.

LET <y> = PA2PDF(<x>,<gamma>,<a>,<loc>,<scale>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, a number, or a parameter;
            <gamma> is a number or parameter that specifies the tail length shape parameter;
            <a> is a number or parameter that specifies the optional lower bound shape parameter;
            <loc> is a number or parameter that specifies the optional location parameter;
            <scale> is a number or parameter that specifies the optional scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed Pareto pdf value is saved;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

The a, loc, and scale parameters are all optional.

LET A = PA2PDF(3,1.5)
LET A = PA2PDF(3,1.5,0.5)
LET X2 = PA2PDF(X1,GAMMA,A)
PLOT PA2PDF(X,GAMMA,A) FOR X = 0 0.01 10

The Pareto distribution of the second kind can be extended with location and scale parameters by using the relationship

Pareto second kind random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET GAMMA = <value>
LET A = <value>
LET Y = PARETO SECOND KIND RANDOM NUMBERS FOR I = 1 1 N
PARETO SECOND KIND PROBABILITY PLOT Y
PARETO SECOND KIND PROBABILITY PLOT Y X
PARETO SECOND KIND PROBABILITY PLOT Y XLOW XHIGH
PARETO SECOND KIND KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
PARETO SECOND KIND CHI-SQUARE GOODNESS OF FIT Y X
PARETO SECOND KIND CHI-SQUARE GOODNESS OF FIT Y XLOW XHIGH


The following commands can be used to estimate the shape parameters for the Pareto distribution of the second kind:

LET A = <value>
LET GAMMA1 = <value>
LET GAMMA2 = <value>
PARETO SECOND KIND PPCC PLOT Y
PARETO SECOND KIND PPCC PLOT Y X
PARETO SECOND KIND PPCC PLOT Y XLOW XHIGH
PARETO SECOND KIND KS PLOT Y
PARETO SECOND KIND KS PLOT Y X
PARETO SECOND KIND KS PLOT Y XLOW XHIGH


The default values for gamma1 and gamma2 are 0.2 and 10, respectively. Note that only the parameter is estimated for these plots. The default value of A is 1.

Johnson, Kotz, and Balakrishnan (see Reference section below) define Pareto distributions of the first, second, third, and fourth kinds. Dataplot supports Pareto distributions of the first and second kinds.

None

None

PA2CDF	= Compute the Pareto second kind cumulative distribution function.
PA2PPF	= Compute the Pareto second kind percent point function.
PARPDF	= Compute the Pareto probability density function.
GEPPDF	= Compute the generalized Pareto probability density function.
EV1PDF	= Compute the extreme value type I probability density function.
WEIPDF	= Compute the Weibull probability density function.
NORPDF	= Compute the normal probability density function.
LGNPDF	= Compute the lognormal probability density function.
EXPPDF	= Compute the exponential probability density function.

"Continuous Univariate Distributions: Volume 1", 2nd. Ed., Johnson, Kotz, and Balakrishnan, John Wiley, 1994, (chapter 20).

Distributional Modeling, Income Distributions

1995/10

 
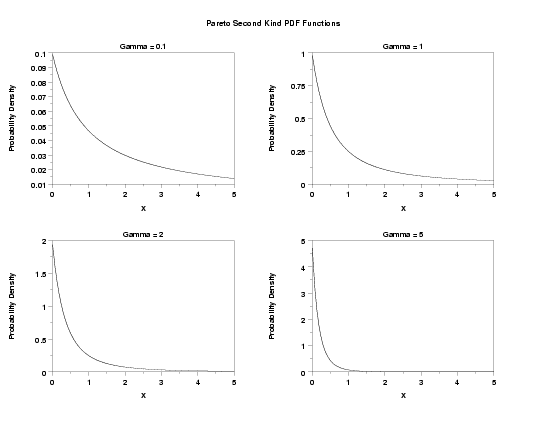
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
CASE ASIS
TITLE CASE ASIS
LABEL CASE ASIS
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
Y1LABEL Probability Density
X1LABEL X
.
LET A = 1
TITLE Gamma = 0.1
PLOT PA2PDF(X,0.1,A) FOR X = 0.01  0.01  5
TITLE Gamma = 1
PLOT PA2PDF(X,1,A) FOR X = 0.01  0.01  5
TITLE Gamma = 2
PLOT PA2PDF(X,2,A) FOR X = 0.01  0.01  5
TITLE Gamma = 5
PLOT PA2PDF(X,5,A) FOR X = 0.01  0.01  5
END OF MULTIPLOT
.
MOVE 50 97
JUSTIFICATION CENTER
TEXT Pareto Second Kind PDF Functions