SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

PARPDF

Name:
    PARPDF (LET)
Type:
    Library Function
Purpose:
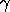    Compute the Pareto probability density function with shape parameters gamma and a.
Description:
    The standard form of the Pareto probability density function is:

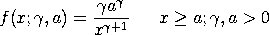
      f(x;gamma,a) = gamma*a**gamma/(x**(gamma+1)) x >= a, a, gamma > 0

    with gamma and a denoting the tail length shape parameter and the lower bound parameter, respectively. The default value of a is 1.

    Note that although the a parameter is typically called a location parameter (and it is in the sense that it defines the lower bound), it is not a location parameter in the technical sense that the following relation does not hold:

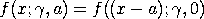
      f(x;gamma,a) = f((x-a);gamma,0)

    For this reason, Dataplot treats a as a shape parameter. In Dataplot, the a shape parameter is optional with a default value of 1.

Syntax:
    LET <y> = PARPDF(<x>,<gamma>,<a>,<loc>,<scale>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a variable, a number, or a parameter;
                <gamma> is a number or parameter that specifies the tail length shape parameter;
                <a> is a number or parameter that specifies the optional lower bound shape parameter;
                <loc> is a number or parameter that specifies the optional location parameter;
                <scale> is a number or parameter that specifies the optional scale parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed Pareto pdf value is saved;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.

    The a, loc, and scale parameters are all optional.

Examples:
    LET A = PARPDF(3,1.5)
    LET A = PARPDF(3,1.5,2)
    LET Y = PARPDF(X,GAMMA,A,LOC,SCALE)
Note:
    The Pareto distribution can be extended with location and scale parameters using the relationship

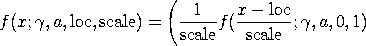
      f(x;gamma,a,loc,scale) = (1/scale)*f(x;gamma,a,0,1)

    Most applications of the Pareto distribution use the standard form (i.e., location = 0 and scale = 1).

Note:
    Pareto random numbers, probability plots, and goodness of fit tests can be generated with the commands:

      LET GAMMA = <value>
      LET A = <value>
      LET Y = PARETO RANDOM NUMBERS FOR I = 1 1 N
      PARETO PROBABILITY PLOT Y
      PARETO KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
      PARETO CHI-SQUARE GOODNESS OF FIT Y

    The following commands can be used to estimate the shape parameters for the Pareto distribution:

      LET GAMMA1 = <value>
      LET GAMMA2 = <value>
      LET A = <value>
      PARETO PPCC PLOT Y
      PARETO KS PLOT Y

    The default values for gamma1 and gamma2 are 0.2 and 10, respectively. Note that only the gamma parameter is estimated for these plots. The default value of A is 1. If the value of A is greater than the data minimum, then it is automatically set to the data minimum.

    You can generate maximum likelihood estimates for the Pareto distribution with the command

      PARETO MAXIMUM LIKELIHOOD Y

    The maximum likelihood estimate of the lower bound parameter is:

      ahat = minimum X(i)

    This estimate is used in the following equation to find the maximum likelihood estimate of the tail length parameter:

      alphahat = n/SUM[i=1 to n][LOG(x(i)/khat)]
Default:
    None
Synonyms:
    None
Related Commands:
    PARCDF = Compute the Pareto cumulative distribution function.
    PARCHAZ = Compute the Pareto cumulative hazard function.
    PARHAZ = Compute the Pareto hazard function.
    PARPPF = Compute the Pareto percent point function.
    GEPPDF = Compute the generalized Pareto probability density function.
    EV1PDF = Compute the extreme value type I probability density function.
    WEIPDF = Compute the Weibull probability density function.
    EXPPDF = Compute the exponential probability density function.
Reference:
    "Continuous Univariate Distributions: Volume 1", Second Edition, Johnson, Kotz, and Balakrishnan, Wiley, 1994, chapter 19.
Applications:
    Distributional Modeling
Implementation Date:
    1994/4
Program: 
     
MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 95
MULTIPLOT SCALE FACTOR 2
.
CASE ASIS
TITLE CASE ASIS
LABEL CASE ASIS
TITLE DISPLACEMENT 2
Y1LABEL DISPLACEMENT 15
X1LABEL DISPLACEMENT 12
Y1LABEL Probability Density
X1LABEL X
.
TITLE Gamma = 1
PLOT PARPDF(X,1) FOR X = 1 0.1 10
TITLE Gamma = 2
PLOT PARPDF(X,2) FOR X = 1 0.1 10
TITLE Gamma = 5
PLOT PARPDF(X,5) FOR X = 1 0.1 10
TITLE Gamma = 0.5
PLOT PARPDF(X,0.5) FOR X = 1 0.1 10
END OF MULTIPLOT
.
MOVE 50 97
JUSTIFICATION CENTER
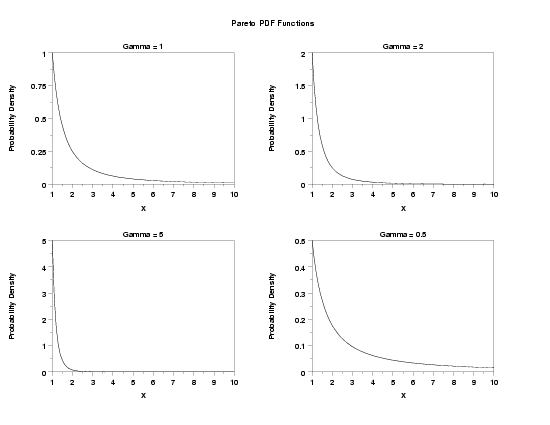
TEXT Pareto PDF Functions
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to [email protected].