SED navigation bar go to SED home page go to Dataplot home page go to NIST home page SED Home Page SED Staff SED Projects SED Products and Publications Search SED Pages
Dataplot Vol 2 Vol 1

QBIPPF

Name:
    QBIPPF (LET)
Type:
    Library Function
Purpose:
    Compute the quasi-binomial type I percent point function.
Description:
    The quasi-binomial type I distribution has the following probability mass function:

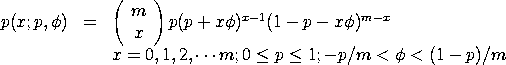
      p(x;p,phi) = (m x)*p*(p + x*phi)**(x-1)*(1-p-x*phi)**(m-x) x = 0, 1, 2, ..., m; 0 <= p <= 1; -p/m < phi < (1-p)/m

    with p, phi, and m denoting the shape parameters.

    The quasi-binomial type I distribution is used to model Bernoulli trials. The parameter p denotes the initial probability of success, m denotes the number of Bernoulli trials, and phi denotes how the probability of success increases or decreases with the number of successes. Specificially, when phi = 0, the quasi-binomial type I distribution reduces to the binomial distribution. When phi ≠ 0, the probability of success in the xth trial becomes

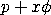
      p + x*phi

    The cumulative distribution function is computed using the following recurrence relation given by Consul and Famoye:

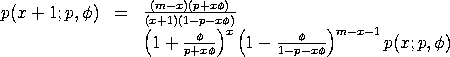
      p(x+1) = {(m-x)*(p+x*phi)/((x+1)*(1-p-x*phi))}* (1 + phi/(p+x*phi))**x*(1 - phi/(1-p-x*phi))**(m-x-1)*p(x)

    The percent point function is computed by summing the cumulative distribution function until the appropriate probability is obtained.

Syntax:
    LET <y> = QBIPPF(<x>,<p>,<theta>,<beta>)
                            <SUBSET/EXCEPT/FOR qualification>
    where <x> is a variable, number, or parameter in the interval (0,1);
                <p> is a number, parameter, or variable in the range (0,1) that specifies the first shape parameter;
                <phi> is a number, parameter, or variable that specifies the second shape parameter;
                <m> is a number, parameter, or variable that specifies the third shape parameter;
                <y> is a variable or a parameter (depending on what <x> is) where the computed quasi binomial type I ppf value is stored;
    and where the <SUBSET/EXCEPT/FOR qualification> is optional.
Examples:
    LET A = QBIPPF(0.95,0.5,0.005,20)
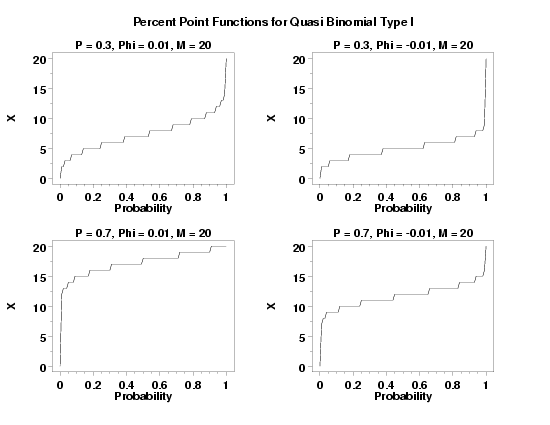
    LET Y = QBIPPF(P,0.7,0.01,20)
    PLOT QBIPPF(P,0.3,0.005,20) FOR P = 0 0.01 1
Default:
    None
Synonyms:
    None
Related Commands:
    QBICDF = Compute the quasi-binomial type I cumulative distribution function.
    QBIPDF = Compute the quasi-binomial type I probability mass function.
    BINPDF = Compute the binomial probability mass function.
    BBNPDF = Compute the beta-binomial probability mass function.
    NBPDF = Compute the negative binomial probability mass function.
Reference:
    Consul and Famoye (2006), "Lagrangian Probability Distribution", Birkhauser, pp. 70-80.
Applications:
    Distributional Modeling
Implementation Date:
    2006/8
Program: 
     
title size 3
tic label size 3
label size 3
legend size 3
height 3
x1label displacement 12
y1label displacement 15
.
multiplot corner coordinates 0 0 100 95
multiplot scale factor 2
label case asis
title case asis
case asis
tic offset units screen
tic offset 3 3
title displacement 2
x1label Probability
y1label X
.
xlimits 0 1
major xtic mark number 6
minor xtic mark number 3
.
multiplot 2 2
.
title P = 0.3, Phi = 0.01, M = 20
plot qbicdf(x,0.3,0.01,20) for x = 0  0.01  1
.
title P = 0.3, Phi = -0.01, M = 20
let phi = -0.01
plot qbicdf(x,0.3,phi,20) for x = 0  0.01  1
.
title P = 0.7, Phi = 0.01, M = 20
plot qbicdf(x,0.7,0.01,20) for x = 0  0.01  1
.
title P = 0.7, Phi = -0.01, M = 20
let phi = -0.01
plot qbicdf(x,0.7,phi,20) for x = 0  0.01  1
.
end of multiplot
.
justification center
move 50 97
text Percent Point Functions for Quasi Binomial Type I
    plot generated by sample program

Date created: 8/23/2006
Last updated: 8/23/2006
Please email comments on this WWW page to alan.heckert@nist.gov.