QN SCALE

QN SCALE (LET)

Let Subcommand

Compute the Q_n scale estimate for a variable.

Mosteller and Tukey (see Reference section below) define two types of robustness:
1. resistance means that changing a small part, even by a large amount, of the data does not cause a large change in the estimate

2. robustness of efficiency means that the statistic has high efficiency in a variety of situations rather than in any one situation. Efficiency means that the estimate is close to optimal estimate given that we know what distribution that the data comes from. A useful measure of efficiency is:
   Efficiency = (lowest variance feasible)/ (actual variance)

Many statistics have one of these properties. However, it can be difficult to find statistics that are both resistant and have robustness of efficiency.

The most common estimate of scale, the standard deviation, is the most efficient estimate of scale if the data come from a normal distribution. However, the standard deviation is not robust in the sense that changing even one value can dramatically change the computed value of the standard deviation (i.e., poor resistance). In addition, it does not have robustness of efficiency for non-normal data.

The median absolute deviation (MAD) and interquartile range are the two most commonly used robust alternatives to the standard deviation. The MAD in particular is a very robust scale estimator. However, the MAD has the following limitations:

1. It does not have particularly high efficiency for data that is in fact normal (37%). In comparison, the median has 64% efficiency for normal data.

2. The MAD statistic also has an implicit assumption of symmetry. That is, it measures the distance from a measure of central location (the median).

Rousseeuw and Croux proposed the Q_n estimate of scale as an alternative to the MAD. It shares desirable robustness properties with MAD (50% breakdown point, bounded influence function). In addition, it has significantly better normal efficiency (82%) and it does not depend on symmetry.

The Qn scale estimate is motivated by the Hodges-Lehmann estimate of location:

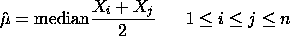
An analogous scale estimate can be obtained by replacing pairwise averages with pairwised distances:

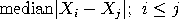
This estimate has high efficiency for normal data (86%), but a breakdown point of only 29%. Rousseeuw and Croux proposed the following variation of this statistic:

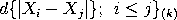
where d is a constant factor and k = which is approximately /4 . The value of h is [n/2]+1 (i.e., roughly half the number of obserations). In words, we take kth order statistic of the interpoint distances. The value of d is choosen to make Q_n a consistent estimator of scale. We use the value 2.2219 since this is the value that makes Q_n a consistent estimator for normal data.

The Rousseeuw and Croux article (see the Reference section below) discusses the properties of the Q_n estimate in detail.

LET <par> = QN SCALE <y>             <SUBSET/EXCEPT/FOR qualification>
where <y> is the response variable;
            <par> is a parameter where the computed Q_n estimate is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

LET A = QN SCALE Y1
LET A = QN SCALE Y1 SUBSET TAG > 2

Dataplot uses code provided by Rousseeuw and Croux to compute the Q_n estimate. This algorithm uses an efficient computational method for computing Q_n.

The Rousseeuw and Croux article also proposes the S_n scale estimate. The article discusses the properties of both estimators in detail.

In addition, the Qn statistic is supported for the following plots and commands
QN SCALE PLOT Y X
CROSS TABULATE QN SCALE PLOT Y X1 X2
BOOTSTRAP QN SCALE PLOT Y
JACKNIFE QN SCALE PLOT Y
DEX QN SCALE PLOT Y X1 ... XK
QN SCALE BLOCK PLOT Y X1 ... XK
QN SCALE INFLUENCE CURVE Y
QN SCALE INTERACTION PLOT Y X1 X2


TABULATE QN SCALE Y X
CROSS TABULATE SN Y X1 X2
LET Z = CROSS TABULATE QN SCALE Y X1 X2
LET Y = MATRIX COLUMN QN SCALE M
LET Y = MATRIX ROW QN SCALE M

None

None

SN SCALE	= Compute the Sn scale estimate of a variable.
MEDIAN ABSOLUTE DEVIATION	= Compute the median absolute deviation of a variable.
INTERQUARTILE RANGE	= Compute the interquartile range of a variable.
STANDARD DEVIATION	= Compute the standard deviation of a variable.
DIFFERENCE OF QN	= Compute the difference of the Qn scale estimates between two variables.
STATISTIC PLOT	= Generate a statistic versus subset plot.
CROSS TABULATE PLOT	= Generate a statistic versus subset plot (two subset variables).
BOOTSTRAP PLOT	= Generate a bootstrap plot for a statistic.

"Alternatives to the Median Absolute Deviation", Peter J. Rousseuw and Christophe Croux, Journal of the American Statistical Association, December, 1993, Vol. 88, No. 424, pp. 1273-1283.

"Data Analysis and Regression: A Second Course in Statistics", Mosteller and Tukey, Addison-Wesley, 1977, pp. 203-209.

Data Analysis

2003/4

MULTIPLOT 2 2
MULTIPLOT CORNER COORDINATES 0 0 100 100
MULTIPLOT SCALE FACTOR 2
X1LABEL DISPLACEMENT 12
.
LET Y1 = NORMAL RANDOM NUMBERS FOR I = 1 1 200
LET SIGMA = 1
LET Y2 = LOGNORMAL RANDOM NUMBERS FOR I = 1 1 200
.
BOOTSTRAP SAMPLES 500
BOOTSTRAP QN SCALE PLOT Y1
X1LABEL B025 = ^B025, B975=^B975
HISTOGRAM YPLOT
X1LABEL
.
BOOTSTRAP QN SCALE PLOT Y2
X1LABEL B025 = ^B025, B975=^B975
HISTOGRAM YPLOT
.
END OF MULTIPLOT
JUSTIFICATION CENTER
MOVE 50 96
TEXT QN SCALE BOOTSTRAP: NORMAL
MOVE 50 46
TEXT QN SCALE BOOTSTRAP: LOGNORMAL