

|
RUKHIN 1 TESTName:
with p1, p2, and p3 denoting the three binomial proportions.
with pi xi, and ni denoting the binomial proportion, the number of successes and the number of trials for the i-th binomial proportion. The computed test statistic is
and the associated standard error is
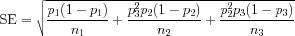
The p-value for a lower tailed test is
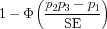
The p-value for an upper tailed test is
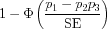
The p-value for a two tailed test is
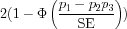
The confidence interval is
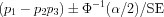
Although this is a fairly specialized test, it does have applicability in the following test scenario. Suppose we are testing scanning devices to see if they can detect certain radionuclides. Further suppose that in one case we have a "primary" screening device and then a "secondary" screening device. For example, the "primary" device may be an alarm which then sends the object to a more accurate (but more costly or more time consuming) device to perform an id. In this case, the binomial success for the primary device is that it alarms when the radionuclide is present and the binomial success for the secondary device is that it returns the correct id. The RUKHIN 1 test could then be used to compare the performance of the primary/secondary device relative to using the secondary device only. In this testing scenario, it is common for the primary device to be "moving" while the secondary device is typically "stationary". So the more accurate device may not perform as well when it is used as a primary device relative to its use as a secondary device.
<p1> <n1> <p2> <n2> <p3> <n3> <alpha> <SUBSET/EXCEPT/FOR qualification> where <p1> is constant, parameter, or variable that contains the proportion of successes for the first sample; <n1> is constant, parameter, or variable that contains the number of trials for the first sample; <p2> is constant, parameter, or variable that contains the proportion of successes for the second sample; <n2> is constant, parameter, or variable that contains the number of trials for the second sample; <p3> is constant, parameter, or variable that contains the proportion of successes for the third sample; <n3> is constant, parameter, or variable that contains the number of trials for the third sample; <alpha> is constant or parameter that contains the significance level; <pval> contains the returned p-value; <lowlim> contains the computed lower confidence limit; <upplim> contains the computed upper confidence limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax performs a two-tailed hypothesis test. The <p1> <n1>, <p2>, <n2>, <p3>, and <n3> arguments can be either parameters or variables. If they are variables, then the variables must have the same number of elements. The <alpha> argument is always assumed to be either a constant or a parameter. If the arguments are all parameters, then <pval>, <lowlim>, and <upplim> will be parameters. Otherwise, they will be variables.
<p1> <n1> <p2> <n2> <p3> <n3> <alpha> <SUBSET/EXCEPT/FOR qualification> where <p1> is constant, parameter, or variable that contains the proportion of successes for the first sample; <n1> is constant, parameter, or variable that contains the number of trials for the first sample; <p2> is constant, parameter, or variable that contains the proportion of successes for the second sample; <n2> is constant, parameter, or variable that contains the number of trials for the second sample; <p3> is constant, parameter, or variable that contains the proportion of successes for the third sample; <n3> is constant, parameter, or variable that contains the number of trials for the third sample; <alpha> is constant or parameter that contains the significance level; <pval> contains the returned p-value; <lowlim> contains the computed lower confidence limit; <upplim> contains the computed upper confidence limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax performs a lower-tailed hypothesis test. However, the confidence limits correspond to the two-tailed test. The <p1> <n1>, <p2>, <n2>, <p3>, and <n3> arguments can be either parameters or variables. If they are variables, then the variables must have the same number of elements. The <alpha> argument is always assumed to be either a constant or a parameter. If the arguments are all parameters, then <pval>, <lowlim>, and <upplim> will be parameters. Otherwise, they will be variables.
<p1> <n1> <p2> <n2> <p3> <n3> <alpha> <SUBSET/EXCEPT/FOR qualification> where <p1> is constant, parameter, or variable that contains the proportion of successes for the first sample; <n1> is constant, parameter, or variable that contains the number of trials for the first sample; <p2> is constant, parameter, or variable that contains the proportion of successes for the second sample; <n2> is constant, parameter, or variable that contains the number of trials for the second sample; <p3> is constant, parameter, or variable that contains the proportion of successes for the third sample; <n3> is constant, parameter, or variable that contains the number of trials for the third sample; <alpha> is constant or parameter that contains the significance level; <pval> contains the returned p-value; <lowlim> contains the computed lower confidence limit; <upplim> contains the computed upper confidence limit; and where the <SUBSET/EXCEPT/FOR qualification> is optional. This syntax performs an upper-tailed hypothesis test. However, the confidence limits correspond to the two-tailed test. The <p1> <n1>, <p2>, <n2>, <p3>, and <n3> arguments can be either parameters or variables. If they are variables, then the variables must have the same number of elements. The <alpha> argument is always assumed to be either a constant or a parameter. If the arguments are all parameters, then <pval>, <lowlim>, and <upplim> will be parameters. Otherwise, they will be variables.
LET PVAL AL AU = RUKHIN 1 LOWER TAILED TEST ... P1 N1 P2 N2 P3 N3 ALPHA LET PVAL AL AU = RUKHIN 1 UPPER TAILED TEST ... P1 N1 P2 N2 P3 N3 ALPHA
LET P1 = 0.8
LET N2 = 40
LET P2 = 0.95
LET N2 = 40
LET P3 = 0.6
LET N3 = 40
LET ALPHA = 0.90
.
LET PVAL AL AU = RUKHIN 1 TEST P1 N1 P2 N2 P3 N3 ALPHA
The returned values of PVAL, AL, and AU are
0.0204, 0.0668, and 0.3932, respectively.
Date created: 10/5/2010 |