SEMPDF

SEMPDF (LET)

Library Function

Compute the semi-circular probability density function.

The semi-circular distribution is the distribution onto one axis of the points uniformly distributed within the unit circle. As such, it is useful for testing 2-dimensional uniformity.

The probability density function for the semi-circular distribution is:

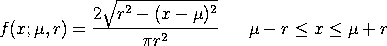
with and r denoting the location and scale parameters, respectively. The scale parameter, r, is the radius of the semi-circle (or ellipse if r not equal to 1).

The case where = 0 and r = 1 is referred to as the standard semi-circular distribution and has the following probability density function:

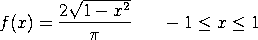
This distribution has mean 0 and standard deviation r/4.

LET <y> = SEMPDF(<x>,<mu>,<r>)
                        <SUBSET/EXCEPT/FOR qualification>
where <x> is a variable, number, or parameter;
            <mu> is a variable, number, or parameter that specifies the location parameter;
            <r> is a variable, number, or parameter that specifies the scale parameter;
            <y> is a variable or a parameter (depending on what <x> is) where the computed semi-circular pdf value is stored;
and where the <SUBSET/EXCEPT/FOR qualification> is optional.

If <mu> and <r> are omitted, they default to 0 and 1, respectively.

LET A = SEMPDF(0.5)
LET A = SEMPDF(1.2,0,5)
LET X2 = SEMPDF(X1)

Semi-circular random numbers, probability plots, and goodness of fit tests can be generated with the commands:
LET Y = SEMI-CIRCULAR RANDOM NUMBERS FOR I = 1 1 N
SEMI-CIRCULAR PROBABILITY PLOT Y
SEMI-CIRCULAR PROBABILITY PLOT Y2 X2
SEMI-CIRCULAR PROBABILITY PLOT Y3 XLOW XHIGH
SEMI-CIRCULAR KOLMOGOROV SMIRNOV GOODNESS OF FIT Y
SEMI-CIRCULAR CHI-SQUARE GOODNESS OF FIT Y2 X2
SEMI-CIRCULAR CHI-SQUARE GOODNESS OF FIT Y3 XLOW XHIGH


The location and scale estimates can be obtained from the probability plot (location = PPA0 and scale = PPA1).

The BOOTSTRAP DISTRIBUTION command can be used to find uncertainty intervals for the location and scale parameters based on the probability plot.

None

None

SEMCDF	= Compute the semi-circular cumulative distribution function.
SEMPPF	= Compute the semi-circular percent point function.
UNIPDF	= Compute the uniform probability density function.
UNICDF	= Compute the uniform cumulative distribution function.
UNIPPF	= Compute the uniform percent point function.
NORCDF	= Compute the normal cumulative distributoin function.
NORPDF	= Compute the normal probability density function.
NORPPF	= Compute the normal percent point function.

Johnson and Kotz (1970), Continuous Univariate Distributions - 2, Houghton Mifflin, (chapter 25).

Filliben (1969), Simple and Robust Linear Estimation of the Location Parameter of a Symmetric Distribution, unpublished Ph.d dissertation, Princeton University, (pp. 21-44, 229-231).

Distributional Modeling

94/4: Implemented for the standard case
2006/10: Updated to support the general case

 
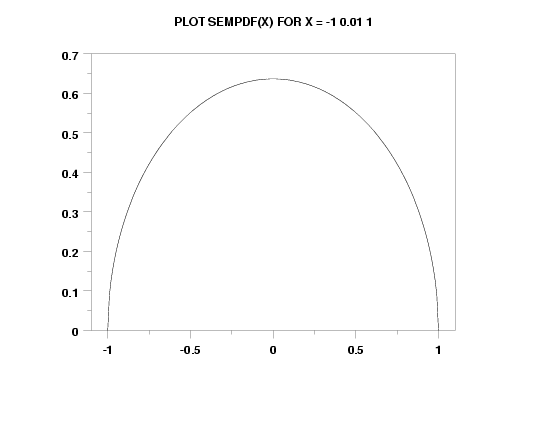
XLIMITS -1 1
XTIC OFFSET 0.1 0.1
TITLE AUTOMATIC
PLOT SEMPDF(X) FOR X = -1 0.01 1